题目内容
(14分)如图所示,机器人海宝按照以下程序运行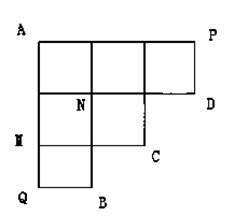
1从A出发到达点B或C或D,到达点B、C、D之一就停止;
②每次只向右或向下按路线运行;
③在每个路口向下的概率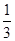 ;
;
④到达P时只向下,到达Q点只向右.
(1)求海宝过点从A经过M到点B的概率,求海宝过点从A经过N到点C的概率;
(2)记海宝到点B、C、D的事件分别记为X=1,X=2,X=3,求随机变量X的分布列及期望.
(1)从A过M到B概率为 ;从A过N到C的概率为
;从A过N到C的概率为 ;(2)
;(2) ;
; ;
;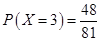 ;
;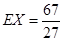 .
.
解析试题分析:(1)从A过M到B,先有两次向下(概率为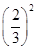 ),再有一次向下与一次向右组合,由乘法原理可得所求概率;同理从A过N到C,需要经过两次向下和两次向右的组合,由乘法原理可得所求概率为
),再有一次向下与一次向右组合,由乘法原理可得所求概率;同理从A过N到C,需要经过两次向下和两次向右的组合,由乘法原理可得所求概率为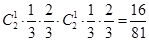 ;(2)先分别求出
;(2)先分别求出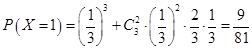 ;
;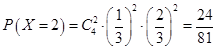 ;
; 的值,再利用离散型随机变量期望公式求随机变量X的期望.
的值,再利用离散型随机变量期望公式求随机变量X的期望.
试题解析:向下概率为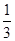 ,则不向下概率为
,则不向下概率为 .
.
(1)从A过M到B,先有两次向下,和有一次向下与一次向右组合其概率为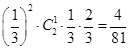 ;
;
从A过M到C,概率为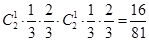 . (7分)
. (7分)
(2)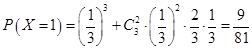 ;
;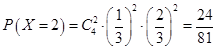 ;
; ;
;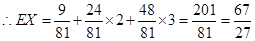 . (14分)
. (14分)
考点:1.独立重复试验型事件发生的概率的计算;2.离散型随机变量期望的计算.

练习册系列答案
相关题目

 ,
,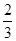 ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.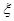 ,求
,求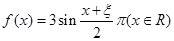 是偶函数”为事件D,求事件D发生的概率.
是偶函数”为事件D,求事件D发生的概率.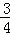 、
、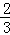 、
、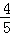 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场. ,求
,求
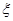 表示乙校中选出的“高个子”人数,试求出
表示乙校中选出的“高个子”人数,试求出
 的值;
的值;