题目内容
在一个盒子里装有6枝圆珠笔,其中3枝一等品,2枝二等品,1枝三等品.
(1)从盒子里任取3枝恰有1枝三等品的概率多大?;
(2)从盒子里任取3枝,设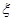 为取出的3枝里一等品的枝数,求
为取出的3枝里一等品的枝数,求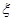 的分布列及数学期望.
的分布列及数学期望.
(1) ;(2)分布列见解析,
;(2)分布列见解析, .
.
解析试题分析:(1)先求出从6枝圆珠笔中任取3支的事件的总数A,再求出恰有1枝是三等品的事件的总数B,用B除以A即是所求的概率;(2)先判断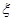 的所有可能的取值,再求出
的所有可能的取值,再求出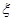 取每个值时对应的概率,根据分布列的列法将所求的概率与对应的
取每个值时对应的概率,根据分布列的列法将所求的概率与对应的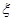 的值分别填入表格,列出分布列,根据分布列中的
的值分别填入表格,列出分布列,根据分布列中的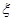 的值及其对应的概率以及公式
的值及其对应的概率以及公式 求数学期望.
求数学期望.
试题解析:(1) ..2分
..2分 4分
4分
(2)  5分
5分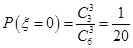 ,
, 
 ,
,
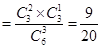 ,
,
 . .9分
. .9分
所以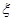 的分布列是:
的分布列是: 10分
10分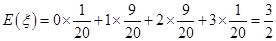 . 12分
. 12分
考点:1.随机事件的概率;2.离散型随机变量及其应用;3.离散型随机变量的分布列与数学期望

练习册系列答案
相关题目
一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:
| 买饭时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
(Ⅰ)求第2分钟末没有人买晚饭的概率;
(Ⅱ)估计第三个学生恰好等待4分钟开始买饭的概率.
德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
| 课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 |
| 合格的概率 |  |  |  |  |
(2)记
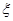 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求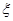 的分布列及期望
的分布列及期望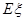 .
. 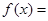
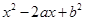 (
(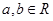 ),若
),若 是从区间
是从区间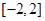 中随机抽取的一个数,
中随机抽取的一个数, 是从区间
是从区间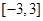 中随机抽取的一个数,求方程
中随机抽取的一个数,求方程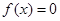 没有实数根的概率.
没有实数根的概率. ,
,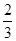 ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.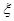 ,求
,求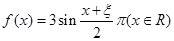 是偶函数”为事件D,求事件D发生的概率.
是偶函数”为事件D,求事件D发生的概率. 的一元二次方程
的一元二次方程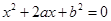 .
. 是从
是从 、
、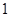 、
、 、
、 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从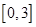 任取的一个数,
任取的一个数,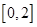 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.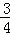 、
、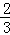 、
、 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场. ,求
,求