题目内容
20.已知数列{an}的首项a1=1,an+1=$\frac{3{a}_{n}}{{a}_{n}+1}$,n∈N+.(Ⅰ)证明:数列{$\frac{1}{{a}_{n}}-\frac{1}{2}$}是等比数列;
(Ⅱ)求数列{$\frac{2n}{{a}_{n}}$}的前n项和Sn.
分析 (Ⅰ)由题意化简递推公式后,代入$\frac{1}{{a}_{n+1}}-\frac{1}{2}$化简后,利用等比数列的定义即可证明结论;
(Ⅱ)由(Ⅰ)和等比数列的通项公式求出an,利用错位相减法、分组求和法、等差、等比数列的前n项和公式,求出数列的前n项和Sn.
解答 证明:(Ⅰ)由题意得,an+1=$\frac{3{a}_{n}}{{a}_{n}+1}$,则$\frac{1}{{a}_{n+1}}$=$\frac{1}{3}$(1+$\frac{1}{{a}_{n}}$),
∴$\frac{1}{{a}_{n+1}}-\frac{1}{2}$=$\frac{1}{3}$($\frac{1}{{a}_{n}}-\frac{1}{2}$),
又a1=1,则$\frac{1}{{a}_{1}}-\frac{1}{2}=\frac{1}{2}$,
∴数列{$\frac{1}{{a}_{n}}-\frac{1}{2}$}是以$\frac{1}{2}$为首项、$\frac{1}{3}$为公比的等比数列,
∴an=2+(n-1)×$\frac{1}{2}$=$\frac{1}{2}$(n+3),∴$\frac{{a}_{n}}{{2}^{n}}$=$\frac{n+3}{{2}^{n+1}}$,
则${S}_{n}=\frac{4}{{2}^{2}}+\frac{5}{{2}^{3}}+\frac{6}{{2}^{4}}+…+\frac{n+3}{{2}^{n+1}}$,
${\frac{1}{2}S}_{n}=\frac{4}{{2}^{3}}+\frac{5}{{2}^{4}}+\frac{6}{{2}^{5}}+…+\frac{n+3}{{2}^{n+2}}$,
两式相减得,${\frac{1}{2}S}_{n}=\frac{4}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}+…+\frac{1}{{2}^{n+1}}-\frac{n+3}{{2}^{n+2}}$
=$\frac{4}{{2}^{2}}+\frac{\frac{1}{8}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}-\frac{n+3}{{2}^{n+2}}$=$\frac{5}{4}-\frac{n+2}{{2}^{n+1}}$,
∴Sn=$\frac{5}{2}-\frac{n+2}{{2}^{n}}$;
(Ⅱ)由(I)得,$\frac{1}{{a}_{n}}-\frac{1}{2}$=$\frac{1}{2}•\frac{1}{{3}^{n-1}}$,
则$\frac{1}{{a}_{n}}=\frac{1}{2}•\frac{1}{{3}^{n-1}}+\frac{1}{2}$,∴$\frac{2n}{{a}_{n}}$=$\frac{n}{{3}^{n-1}}+n$,
令${T}_{n}=\frac{1}{{3}^{0}}+\frac{2}{{3}^{1}}+\frac{3}{{3}^{2}}+…+\frac{n}{{3}^{n-1}}$,①
$\frac{1}{3}{T}_{n}=\frac{1}{{3}^{1}}+\frac{2}{{3}^{2}}+\frac{3}{{3}^{3}}+…+\frac{n}{{3}^{n}}$,②,
①-②得,$\frac{2}{3}{T}_{n}=\frac{1}{{3}^{0}}+\frac{1}{{3}^{1}}+\frac{1}{{3}^{2}}+…+\frac{1}{{3}^{n-1}}-\frac{n}{{3}^{n}}$
=$\frac{1-\frac{1}{{3}^{n}}}{1-\frac{1}{3}}-\frac{n}{{3}^{n}}$=$\frac{3}{2}-\frac{2n+3}{{2•3}^{n}}$,
则${T}_{n}=\frac{9}{4}-\frac{2n+3}{4•{3}^{n-1}}$,
所以Sn=Tn+1+2+3+…+n=$\frac{9}{4}-\frac{2n+3}{4•{3}^{n-1}}$+$\frac{n(1+n)}{2}$
=$\frac{2{n}^{2}+2n+9}{4}-\frac{2n+3}{4•{3}^{n-1}}$.
点评 本题考查了等比数列的定义、通项公式,等差、等比数列的前n项和公式,以及错位相减法、分组求和法求数列的和,属于中档题.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
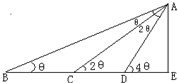 如图在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进15m,至点C处测得顶端A的仰角为2θ,再继续前进5$\sqrt{3}$m至D点,测得顶端A的仰角为4θ,则建筑物AE的高为$\frac{15}{2}$m.
如图在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进15m,至点C处测得顶端A的仰角为2θ,再继续前进5$\sqrt{3}$m至D点,测得顶端A的仰角为4θ,则建筑物AE的高为$\frac{15}{2}$m.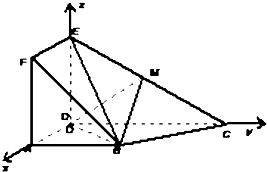 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.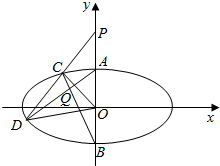 如图,椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,上、下顶点为A,B,点P(0,2)关于直线y=-x的对称点在椭圆M上,过点P的直线l与椭圆M相交于两个不同的点C,D(C在线段PD之间).
如图,椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,上、下顶点为A,B,点P(0,2)关于直线y=-x的对称点在椭圆M上,过点P的直线l与椭圆M相交于两个不同的点C,D(C在线段PD之间).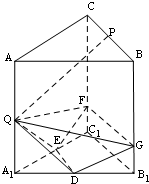 如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3.
如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3.