题目内容
4.△ABC外接圆的半径为1,圆心为O,且$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AO},|\overrightarrow{AB}|=\sqrt{3}|\overrightarrow{OA}|,则\overrightarrow{CA}•\overrightarrow{CB}$的值是1.分析 由题意可得三角形是以角A为直角的直角三角形,解直角三角形求出相应的边和角,代入数量积公式得答案.
解答 解:∵$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AO}$,∴O为BC的中点,
又O为三角形的外心,∴三角形是以角A为直角的直角三角形,
∴OA=1,AB=$\sqrt{3}$,可得CA=1,CB=2,∠BCA=60°,
∴$\overrightarrow{CA}•\overrightarrow{CB}$=$|\overrightarrow{CA}||\overrightarrow{CB}|cos60°$=$1×2×\frac{1}{2}$=1.
故答案为:1.
点评 本题考查平面向量的数量积运算,考查直角三角形中的边角关系,是基础题.

练习册系列答案
相关题目
13.如图,三个边长为2的等边三角形有一条边在同一条直线上,边B3C3上有10个不同的点P1,P2,…P10,记mi=$\overrightarrow{A{B_2}}•\overrightarrow{A{P_i}}$(i=1,2,…,10),则m1+m2+…+m10的值为( )

| A. | 180 | B. | $60\sqrt{3}$ | C. | 45 | D. | $15\sqrt{3}$ |
14.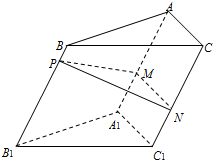 如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
(1)求证:CC1⊥MN;
(2)在任意△DEF中有余弦定理:DE2=DF2+EF2-2DF•EFcos∠DFE.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
(3)在(2)中,我们看到了平面图形中的性质类比到空间图形的例子,这样的例子还有不少.下面请观察平面勾股定理的条件和结论特征,试着将勾股定理推广到空间去.
请在答题纸上完成上表中的类比结论,并给出证明.
 如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.(1)求证:CC1⊥MN;
(2)在任意△DEF中有余弦定理:DE2=DF2+EF2-2DF•EFcos∠DFE.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
(3)在(2)中,我们看到了平面图形中的性质类比到空间图形的例子,这样的例子还有不少.下面请观察平面勾股定理的条件和结论特征,试着将勾股定理推广到空间去.
| 勾股定理的类比 | 三角形ABC | 四面体O-ABC |
| 条件 | AB⊥AC | OA、OB、OC两两垂直 |
| 结论 | AB2+AC2=BC2 | ? |
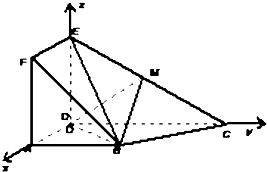 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.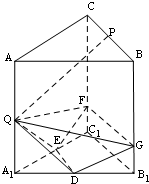 如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3.
如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3.