题目内容
10.在数列{an}中,已知a1=1,Sn=n2an,求通项公式an.分析 利用an+1=Sn+1-Sn,整理出an的递推式,进而用叠乘法求得an.
解答 解:∵Sn=n2an,∴Sn+1=(n+1)2an+1,
两式相减得:an+1=Sn+1-Sn=(n+1)2an+1-n2an,
∴n2an=n(n+2)an+1,即nan=(n+2)an+1,
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n}{n+2}$,即$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n-1}{n+1}$,
∴$\frac{{a}_{n}}{{a}_{n-1}}$•$\frac{{a}_{n-1}}{{a}_{n-2}}$•…•$\frac{{a}_{2}}{{a}_{1}}$•=$\frac{n-1}{n+1}$•$\frac{n-2}{n}$•…•$\frac{1}{3}$=$\frac{2}{n(n+1)}$,
又∵a1=1,∴an=$\frac{n-1}{n+1}$•$\frac{n-2}{n}$•…•$\frac{1}{3}$•1=$\frac{2}{n(n+1)}$,
即数列{an}的通项为:$\frac{2}{n(n+1)}$.
点评 本题主要考查了数列的递推式.数列的递推式是高考中常考的题型,涉及数列的通项公式,求和问题,数列与不等式的综合等问题,注意解题方法的积累,属于中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
18.在△ABC中,E为AC上一点,且$\overrightarrow{AC}=4\overrightarrow{AE}$,P为BE上一点,且$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AC}$(m>0,n>0),则$\frac{1}{m}+\frac{1}{n}$取最小值时,向量$\overrightarrow{a}$=(m,n)的模为( )
| A. | $\frac{{\sqrt{5}}}{4}$ | B. | $\frac{{\sqrt{6}}}{6}$ | C. | $\frac{{\sqrt{5}}}{6}$ | D. | 2 |
5.将函数y=sin2x的图象向左平移φ(0<φ<π)个单位后得函数$y=sin({2x-\frac{π}{3}})$的图象,则φ的值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
2.某校通过随机询问100名性别不同的学生是否能做到“光盘”行动,得到所示联表:
附:K2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$,则下列结论正确的是( )
| 做不到“光盘” | 能做到“光盘” | |
| 男 | 45 | 10 |
| 女 | 30 | 15 |
| P(K2≥k) | 0.10 | 0.05 | 0.01 |
| k | 2.706 | 3.841 | 6.635 |
| A. | 在犯错误的概率不超过1%的前提下,认为“该校学生能否做到‘光盘’与性别无关” | |
| B. | 有99%以上的把握认为“该校学生能否做到‘光盘’与性别有关” | |
| C. | 在犯错误的概率不超过10%的前提下,认为“该校学生能否做到‘光盘’与性别有关” | |
| D. | 有90%以上的把握认为“该校学生能否做到‘光盘’与性别无关” |
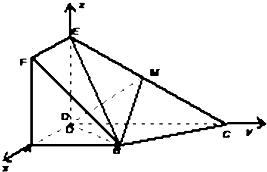 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.