题目内容
设点A为圆 +
+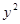 =1上的动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为( )
=1上的动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为( )
 +
+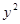 =1上的动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为( )
=1上的动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为( )A. + +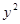 =4; =4; | B.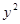 =2 =2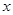 ; ; | C. + +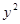 =2; =2; | D.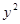 =-2 =-2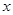 . . |
C
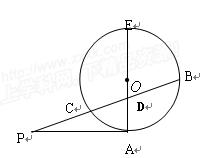
分析:圆(x-1)2+y2=1的圆心为C(1,0),半径为1,根据PA是圆的切线,且|PA|=1,可得|PC|=
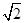 ,从而可求P点的轨迹方程
,从而可求P点的轨迹方程解:设P(x,y),则由题意,圆(x-1)2+y2=1的圆心为C(1,0),半径为1
∵PA是圆的切线,且|PA|=1
∴|PC|=
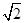
∴P点的轨迹方程为(x-1)2+y2=2
故选C

练习册系列答案
相关题目
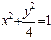
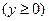 的铁皮截取一个以短轴
的铁皮截取一个以短轴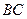 为底的等腰梯形
为底的等腰梯形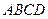 ,问:怎样截才能使所得等腰梯形
,问:怎样截才能使所得等腰梯形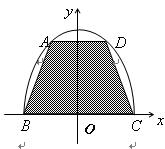
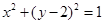 相切,且在每坐标轴上截距相等的距离有( )
相切,且在每坐标轴上截距相等的距离有( )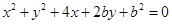 与x轴相切,则b的值为
与x轴相切,则b的值为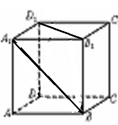
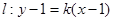 和圆
和圆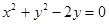 的位置关系是 ( )
的位置关系是 ( )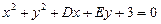 ,圆C关于直线
,圆C关于直线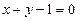 对称,圆心在第二象限,半径为
对称,圆心在第二象限,半径为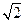
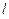 与圆C相切,且在x轴、y轴上的截距相等,求直线
与圆C相切,且在x轴、y轴上的截距相等,求直线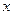 轴上,椭圆C上的点到焦点的最大值为
轴上,椭圆C上的点到焦点的最大值为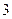 ,最小值为
,最小值为 .
.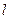 :
: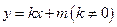 与椭圆交于不同的两点
与椭圆交于不同的两点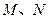 (
(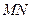 为直径的圆经过椭圆的右顶点
为直径的圆经过椭圆的右顶点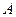 .求证:直线
.求证:直线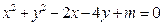 ,若此方程表示圆
,若此方程表示圆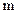 的取值范围
的取值范围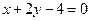 相交于M、N两点,且OM
相交于M、N两点,且OM ON
ON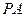 与圆
与圆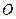 相切于
相切于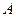 ,不过圆心
,不过圆心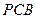 与直径
与直径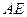 相交于
相交于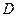 点.已知∠
点.已知∠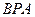 =
=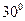 ,
,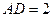 ,
,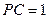 ,则圆
,则圆