题目内容
(本小题满分12分)
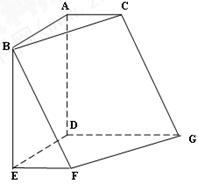
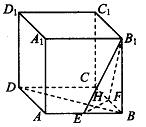
如图,在六面体ABC-DEFG中,平面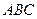 ∥平面
∥平面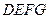 ,
,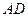 ⊥平面
⊥平面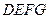 ,
,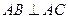 ,
,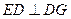 ,
,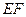 ∥
∥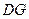 .且
.且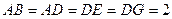 ,
,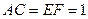 .
.
(1)求证: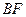 ∥平面
∥平面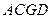 ;
;
(2)求二面角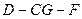 的余弦值.
的余弦值.
如图,在六面体ABC-DEFG中,平面
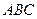 ∥平面
∥平面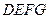 ,
,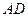 ⊥平面
⊥平面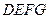 ,
,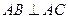 ,
,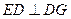 ,
,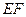 ∥
∥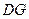 .且
.且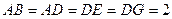 ,
,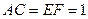 .
.
(1)求证:
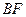 ∥平面
∥平面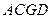 ;
;(2)求二面角
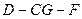 的余弦值.
的余弦值.(1)略(2)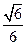
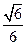

则
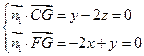 ,
,令
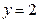 ,则
,则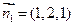 ,
,而平面ADGC的法向量
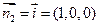
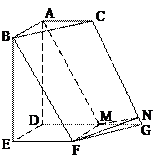 ∴
∴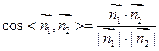 =
=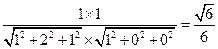
故二面角D-CG-F的余弦值为
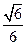 .……………………12分
.……………………12分解法二设DG的中点为M,连接AM、FM,
则由已知条件易证四边形DEFM是平行四边形,
所以MF//DE,且MF=DE
又∵AB//DE,且AB=DE ∴MF//AB,且MF=AB
∴四边形ABMF是平行四边形,即BF//AM,
又BF
 平面ACGD
平面ACGD故 BF//平面A
 CGD……………6分
CGD……………6分(利用面面平行的性质定理证明,可参照给分)
(Ⅱ)由已知AD⊥面DEFG∴DE⊥AD ,DE⊥DG
即DE⊥面ADGC ,
∵MF//DE,且MF=DE , ∴MF⊥面ADGC
在平面ADGC中,过M作MN⊥G
 C,垂足为N,连接NF,则
C,垂足为N,连接NF,则显然∠MNF是所求二面角的平面角.
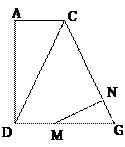 ∵在四边形ADGC中,
∵在四边形ADGC中, AD⊥AC,AD⊥DG,AC=DM=MG=1
AD⊥AC,AD⊥DG,AC=DM=MG=1∴
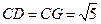 ,∴MN=
,∴MN=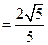
在直角三角形MNF中,MF=2,MN
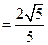
∴
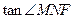 =
=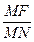 =
=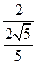 =
=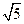 ,
,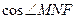 =
=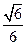
故二面角D-CG-F的余弦值为
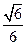 ……………………12分
……………………12分
练习册系列答案
相关题目
 平面ABC ,
平面ABC ,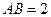 ,已知AE与平面ABC所成的角为
,已知AE与平面ABC所成的角为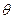 ,
, 且
且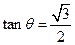 .
.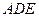 ;
;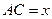 ,
,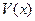 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求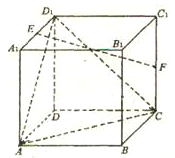
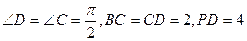 ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将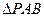 沿AB折到
沿AB折到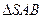 的位置,使
的位置,使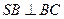 ,点E在SD上,且
,点E在SD上,且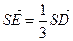 ,如下右图。
,如下右图。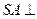 平面ABCD;
平面ABCD;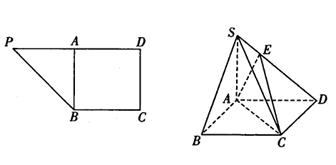 (2)求二面角E—AC—D的正切值;
(2)求二面角E—AC—D的正切值; ,四个顶点在同一个球面上,则此球的表面积为
,四个顶点在同一个球面上,则此球的表面积为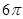
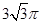
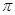
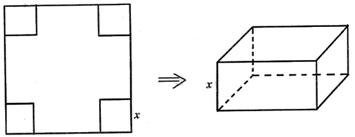
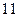 ,其
,其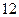 条棱的长度之和为
条棱的长度之和为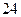 ,则这个长方体的一条
,则这个长方体的一条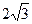
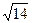
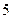
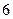
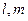 与平面
与平面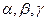 满足:
满足: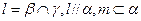 和
和 那么必有( )
那么必有( )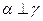 且
且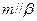
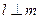
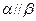 且
且