题目内容
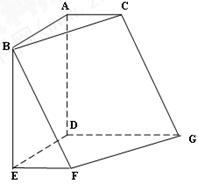
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行
四边形,DC 平面ABC ,
平面ABC ,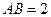 ,已知AE与平面ABC所成的角为
,已知AE与平面ABC所成的角为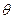 ,
,
 且
且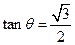 .
.
(1)证明:平面ACD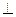 平面
平面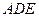 ;
;
(2)记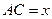 ,
,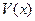 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求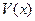 的表达式;
的表达式;
(3)当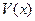 取得最大值时,求二面角D-AB-C的大小.
取得最大值时,求二面角D-AB-C的大小.
四边形,DC
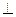 平面ABC ,
平面ABC ,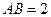 ,已知AE与平面ABC所成的角为
,已知AE与平面ABC所成的角为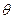 ,
, 且
且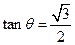 .
.(1)证明:平面ACD
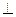 平面
平面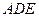 ;
;(2)记
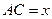 ,
,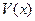 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求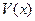 的表达式;
的表达式;(3)当
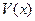 取得最大值时,求二面角D-AB-C的大小.
取得最大值时,求二面角D-AB-C的大小.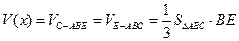
 (
( )
)二面角D-AB-C为60°
解:(1)证明:∵四边形DCBE为平行四边形 ∴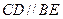 ,
, ---------1分
---------1分
∵DC 平面ABC ,
平面ABC ,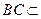 平面ABC ∴
平面ABC ∴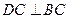 . ----------2分
. ----------2分
∵AB是圆O的直径 ∴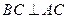 且
且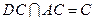
∴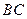
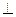 平面ADC.
平面ADC.
∵DE//BC ∴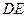
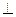 平面ADC ---------------------------------------3分
平面ADC ---------------------------------------3分
又∵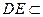 平面ADE ∴平面ACD
平面ADE ∴平面ACD 平面
平面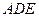 ----------------4分
----------------4分
(2)∵DC 平面ABC ∴
平面ABC ∴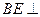 平面ABC
平面ABC
∴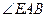 为AE与平面ABC所成的角,即
为AE与平面ABC所成的角,即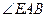 =
=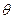 -------------------5分
-------------------5分
在Rt△ABE中,由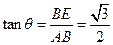 ,
,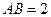 得
得 ------------6分
------------6分
在Rt△ABC中∵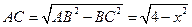 (
(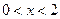 )
)
∴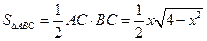 ------------------------------------7分
------------------------------------7分
∴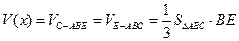
 (
(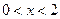 )-------8分
)-------8分
(3)由(2)知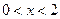
要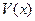 取得最大值,当且仅当
取得最大值,当且仅当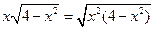 取得最大值,
取得最大值,
∵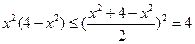 ---------------------------------------------------------9分
---------------------------------------------------------9分
当且仅当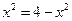 ,即
,即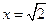 时,“=”成立,
时,“=”成立,
∴当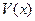 取得最大值时
取得最大值时 ,这时△ACB为等腰直角三角形----------------10分
,这时△ACB为等腰直角三角形----------------10分
 解法1:连结CO,DO
解法1:连结CO,DO
∵AC=BC,DC=DC
∴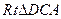 ≌
≌ ∴AD="DB "
∴AD="DB "
又∵O为AB的中点 ∴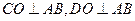
∴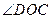 为二面角D-AB-C的平面角------------12分
为二面角D-AB-C的平面角------------12分
在 中 ∵
中 ∵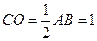 ,
,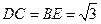
∴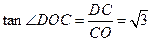 , ∴
, ∴ =
=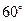
即当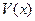 取得最大值时,二面角D-AB-C为60°.--------------------------------14分
取得最大值时,二面角D-AB-C为60°.--------------------------------14分
解法2:以点O为坐标原定,OB为x轴建立空间直角坐标系如图示:
则B(1,0,0),C(0,1,0),D(0,1,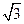 ),
),
∴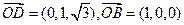 ,
,
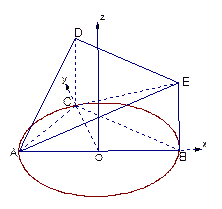 平面ABC的法向量
平面ABC的法向量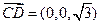 ,---------------------11分
,---------------------11分
设平面ABD的法向量为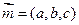
由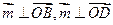 得
得
令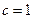 ,则
,则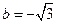 ∴
∴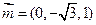 -------------12分
-------------12分
设二面角D-AB-C的大小为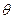 ,则
,则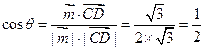
∴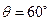 ,即二面角D-AB-C的大小为60°.------------------------------------14分
,即二面角D-AB-C的大小为60°.------------------------------------14分
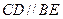 ,
, ---------1分
---------1分∵DC
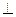 平面ABC ,
平面ABC ,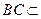 平面ABC ∴
平面ABC ∴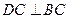 . ----------2分
. ----------2分∵AB是圆O的直径 ∴
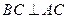 且
且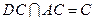
∴
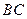
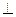 平面ADC.
平面ADC. ∵DE//BC ∴
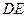
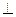 平面ADC ---------------------------------------3分
平面ADC ---------------------------------------3分又∵
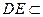 平面ADE ∴平面ACD
平面ADE ∴平面ACD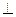 平面
平面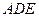 ----------------4分
----------------4分(2)∵DC
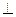 平面ABC ∴
平面ABC ∴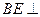 平面ABC
平面ABC∴
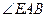 为AE与平面ABC所成的角,即
为AE与平面ABC所成的角,即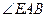 =
=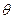 -------------------5分
-------------------5分在Rt△ABE中,由
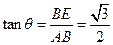 ,
,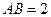 得
得 ------------6分
------------6分在Rt△ABC中∵
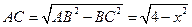 (
(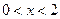 )
)∴
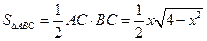 ------------------------------------7分
------------------------------------7分∴
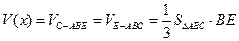
 (
(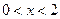 )-------8分
)-------8分(3)由(2)知
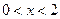
要
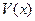 取得最大值,当且仅当
取得最大值,当且仅当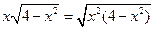 取得最大值,
取得最大值,
∵
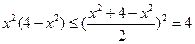 ---------------------------------------------------------9分
---------------------------------------------------------9分当且仅当
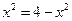 ,即
,即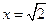 时,“=”成立,
时,“=”成立,∴当
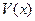 取得最大值时
取得最大值时 ,这时△ACB为等腰直角三角形----------------10分
,这时△ACB为等腰直角三角形----------------10分 解法1:连结CO,DO
解法1:连结CO,DO∵AC=BC,DC=DC
∴
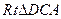 ≌
≌ ∴AD="DB "
∴AD="DB " 又∵O为AB的中点 ∴
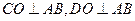
∴
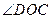 为二面角D-AB-C的平面角------------12分
为二面角D-AB-C的平面角------------12分在
 中 ∵
中 ∵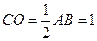 ,
,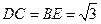
∴
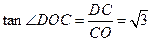 , ∴
, ∴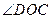 =
=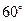
即当
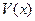 取得最大值时,二面角D-AB-C为60°.--------------------------------14分
取得最大值时,二面角D-AB-C为60°.--------------------------------14分解法2:以点O为坐标原定,OB为x轴建立空间直角坐标系如图示:
则B(1,0,0),C(0,1,0),D(0,1,
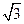 ),
),∴
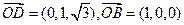 ,
, 平面ABC的法向量
平面ABC的法向量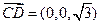 ,---------------------11分
,---------------------11分设平面ABD的法向量为
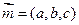
由
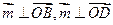 得
得
令
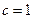 ,则
,则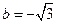 ∴
∴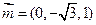 -------------12分
-------------12分设二面角D-AB-C的大小为
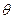 ,则
,则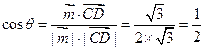
∴
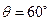 ,即二面角D-AB-C的大小为60°.------------------------------------14分
,即二面角D-AB-C的大小为60°.------------------------------------14分
练习册系列答案
相关题目
 中,
中,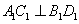 ,
,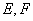 分别是
分别是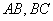 的中点.
的中点.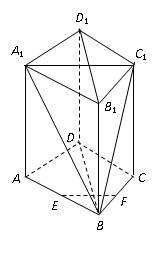
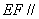 平面
平面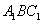 ;
;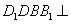 平面
平面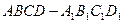 的棱长是2,
的棱长是2,
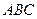 ∥平面
∥平面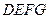 ,
,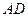 ⊥平面
⊥平面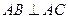 ,
,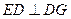 ,
,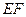 ∥
∥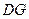 .且
.且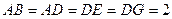 ,
,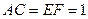 .
.
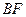 ∥平面
∥平面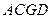 ;
;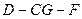 的余弦值.
的余弦值.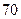 个
个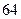 个
个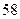 个
个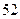 个
个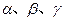 是三个不同的平面,命题“
是三个不同的平面,命题“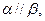 且
且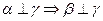 ”是真命题.若把
”是真命题.若把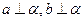 ,则
,则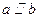 ;②若
;②若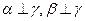 ,则
,则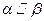 ;
;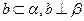 ,则
,则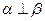 ;④若
;④若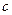 是
是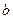 在
在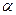 内的射影,
内的射影,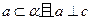 ,则
,则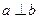 .
.