题目内容
10.已知点P(sinα-cosα,tanα)在第一象限,则在[0,2π]内α的取值范围是( )| A. | ($\frac{π}{2}$,$\frac{3π}{4}$)∪(π,$\frac{5π}{4}$) | B. | ($\frac{π}{4}$,$\frac{π}{2}$)∪(π,$\frac{5π}{4}$) | C. | ($\frac{π}{2}$,$\frac{3π}{4}$)∪($\frac{5π}{4}$,$\frac{3π}{2}$) | D. | ($\frac{π}{4}$,$\frac{π}{2}$)∪($\frac{3π}{4}$,π) |
分析 根据点的坐标与象限之间的关系,结合三角函数的图象和性质进行求解即可.
解答 解:点P(sinα-cosα,tanα)在第一象限,
∴$\left\{\begin{array}{l}{sinα-cosα>0}\\{tanα>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{sinα>cosα}\\{tanα>0}\end{array}\right.$,
∵α∈[0,2π],
∴$\left\{\begin{array}{l}{\frac{π}{4}<α<\frac{5π}{4}}\\{0<α<\frac{π}{2}或π<α<\frac{3π}{2}}\end{array}\right.$,
即$\frac{π}{4}$<α<$\frac{π}{2}$或π<α<$\frac{5π}{4}$,
故∈($\frac{π}{4}$,$\frac{π}{2}$)∪(π,$\frac{5π}{4}$),
故选:B
点评 本题主要考查三角函数符号的判断,根据三角函数的图象和性质是解决本题的关键.

练习册系列答案
相关题目
5.若点P在平面ABC内射影为O,且PA⊥BC,PB⊥AC,则点O为△ABC的( )
| A. | 重心 | B. | 外心 | C. | 内心 | D. | 垂心 |
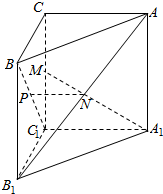 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=$\sqrt{6}$,点P、M、N分别为BC1、CC1、AB1的中点.
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=$\sqrt{6}$,点P、M、N分别为BC1、CC1、AB1的中点. 某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则图中a的值为0.005.
某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则图中a的值为0.005.