题目内容
3.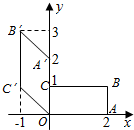 如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍的变换所对应的矩阵.
如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍的变换所对应的矩阵.(Ⅰ)求矩阵M,N;
(Ⅱ)直线l先在矩阵M,再在矩阵N所对应的线性变换作用下像的方程为x+y+1=0.求直线l的方程.
分析 (Ⅰ)设T$\left\{\begin{array}{l}{x′=ax+by}\\{y′=cx+dy}\end{array}\right.$,由题意可得$\left\{\begin{array}{l}{\stackrel{2a=0}{2c=2}}\\{\stackrel{2a+b=-1}{2c+d=3}}\end{array}\right.$解得a,b,c,d的值,即可求得矩阵M,N.
(Ⅱ)设直线l上任一点(x,y)依次在矩阵M,N即矩阵NM所对应的线性变换作用下对应点(x′,y′),可得$\left\{\begin{array}{l}{x′=-2y}\\{y′=3x+3y}\end{array}\right.$代入x′+y′+1=0即可得解.
解答 解:(Ⅰ)设T$\left\{\begin{array}{l}{x′=ax+by}\\{y′=cx+dy}\end{array}\right.$,A(2,0)→A′(0,2),B′(2,1)→B′(-1,3),
∴$\left\{\begin{array}{l}{\stackrel{2a=0}{2c=2}}\\{\stackrel{2a+b=-1}{2c+d=3}}\end{array}\right.$解得$\left\{\begin{array}{l}{\stackrel{a=0}{b=-1}}\\{\stackrel{c=1}{d=1}}\end{array}\right.$,即有M=$(\begin{array}{l}{0}&{-1}\\{1}&{1}\end{array})$,N=$(\begin{array}{l}{2}&{0}\\{0}&{3}\end{array})$…4分
(Ⅱ)NM=$(\begin{array}{l}{2}&{0}\\{0}&{3}\end{array})(\begin{array}{l}{0}&{-1}\\{1}&{1}\end{array})(\begin{array}{l}{0}&{-2}\\{3}&{3}\end{array})$,
设直线l上任一点(x,y)依次在矩阵M,N即矩阵NM所对应的线性变换作用下对应点(x′,y′),
则$\left\{\begin{array}{l}{x′=-2y}\\{y′=3x+3y}\end{array}\right.$代入x′+y′+1=0可得3x+y+1=0,
所以,直线l的方程是3x+y+1=0…7分
点评 本题考查了矩阵变换的性质,矩阵的乘法,属于中档题.

| A. | 直角三角形 | B. | 等腰直角三角形 | C. | 等腰三角形 | D. | 正三角形 |
| A. | [-40,40] | B. | [-30,30] | C. | [-15,15] | D. | [-10,10] |
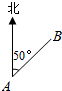 某人沿一条折线段组成的小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角)是50°,距离是3km;从B到C,方位角是110°,距离是3km;从C到D,方位角是140°,距离是($9+3\sqrt{3}$)km.
某人沿一条折线段组成的小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角)是50°,距离是3km;从B到C,方位角是110°,距离是3km;从C到D,方位角是140°,距离是($9+3\sqrt{3}$)km.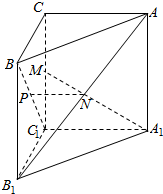 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=$\sqrt{6}$,点P、M、N分别为BC1、CC1、AB1的中点.
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=$\sqrt{6}$,点P、M、N分别为BC1、CC1、AB1的中点.