题目内容
7.设{an}是由正数组成的等差数列,{bn}是由正数组成的等比数列,且a1=b1,a2015=b2015,则必有( )| A. | a1008>b1008 | B. | a1008=b1008 | C. | a1008≥b1008 | D. | a1008≤b1008 |
分析 根据等差数列的等差中项,求出a1008的表达式,由基本不等式,再结合题中条件找出a1008与b1008的关系即可求出答案.
解答 解:由题意可知:a1=b1,a2015=b2015,
且{an}是由正数组成的等差数列,{bn}是由正数组成的等比数列,
则a1008=$\frac{{a}_{1}+{a}_{2015}}{2}$≥$\sqrt{{a}_{1}•{a}_{2015}}$=$\sqrt{{b}_{1}•{b}_{2015}}$=b1008,
故选C.
点评 本题考查了等差数列和等比数列的综合应用,考查了学生的计算能力以及对数列的综合掌握,解题时注意转化思想的运用,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
2.已知函数f(x)=lnx+$\frac{2a}{x}$,a∈R
(1)若函数f(x)在[1,+∞)上是增函数,求实数a的取值范围;
(2)若函数f(x)在[1,e]上的最小值为2,求实数a的取值范围.
(1)若函数f(x)在[1,+∞)上是增函数,求实数a的取值范围;
(2)若函数f(x)在[1,e]上的最小值为2,求实数a的取值范围.
16.复数z=$\frac{-2i}{1+i}$的虚部为( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
17.深圳市某学校为了了解学生使用手机与学习成绩之间的关系,抽查了有手机同学40名,其中成绩为优秀的人数24名,抽查没有手机同学20人,其中成绩为优秀的人数15名,
(1)根据以上数据完成下面的2×2列联表(单位:人)
(2)根据题(1)中表格的数据计算,你有多大的把握,认为学生手机与成绩之间有关系?
(1)根据以上数据完成下面的2×2列联表(单位:人)
| 拥有手机 | 没有手机 | 合计 | |
| 成绩优秀 | |||
| 成绩不优势 | |||
| 合计 |
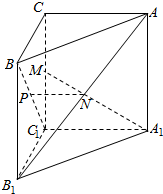 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=$\sqrt{6}$,点P、M、N分别为BC1、CC1、AB1的中点.
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=$\sqrt{6}$,点P、M、N分别为BC1、CC1、AB1的中点.