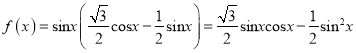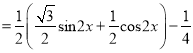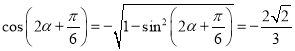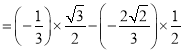题目内容
【题目】已知函数![]() 为偶函数,且函数
为偶函数,且函数![]() 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为![]() .
.
(1)求![]() 的值;
的值;
(2)求函数![]() 的对称轴方程;
的对称轴方程;
(3)当![]() 时,方程
时,方程![]() 有两个不同的实根,求m的取值范围。
有两个不同的实根,求m的取值范围。
【答案】(1)![]() .(2)
.(2)![]() ;(3)
;(3) ![]()
【解析】
(1)根据题意求出φ、ω的值,写出f(x)的解析式,计算![]() 的值;(2)由f(x)写出函数
的值;(2)由f(x)写出函数![]() 的解析式,求出对称轴方程;(3)若f(x)=m有两个不同的实根,则函数y=f(x)与y=m有两个不同的交点,令t=2x,
的解析式,求出对称轴方程;(3)若f(x)=m有两个不同的实根,则函数y=f(x)与y=m有两个不同的交点,令t=2x,![]() ,则
,则![]() 的图像与
的图像与![]() 有两个不同交点即可求结果.
有两个不同交点即可求结果.
解:(1)![]() 是偶函数,则φ﹣
是偶函数,则φ﹣![]() =
=![]() +kπ(k∈Z),
+kπ(k∈Z),
解得φ=![]() +kπ(k∈Z),
+kπ(k∈Z),
又因为0<φ<π,所以φ=![]() ,
,
所以![]() =2cosωx;
=2cosωx;
由题意得![]() =2
=2![]() ,所以ω=2;
,所以ω=2;
故f(x)=2cos 2x,
因此![]() =2cos
=2cos ![]() =
=![]() ;
;
(2)由f(x)=2cos 2x,
得![]() =
=![]() ,
,
所以,![]() ,
,
即![]() ,
,
所以函数![]() 的对称轴方程为
的对称轴方程为![]() ;
;
(3)若f(x)=m有两个不同的实根,则函数y=f(x)与y=m有两个不同的交点,函数y=f(x)=2cos 2x,令t=2x,![]() ,则
,则![]() 的图像与
的图像与![]() 有两个不同交点,由图像知
有两个不同交点,由图像知![]()
即m的取值范围是![]() .
.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目