题目内容
【题目】【2018河北保定市高三上学期期末调研】如图,四面体![]() 中,
中, ![]() 、
、![]() 分别
分别![]() 、
、![]() 的中点,
的中点, ![]() ,
, ![]() .
.
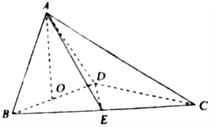
(I)求证: ![]() 平面
平面![]() ;
;
(II)求异面直线![]() 与
与![]() 所成角的余弦值的大小;
所成角的余弦值的大小;
(III)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(I)证明见解析;(II)![]() ;(III)
;(III)![]() .
.
【解析】试题分析:(1)由已知条件得出![]() ,由计算得出
,由计算得出![]() ,得出
,得出![]() ,再由线面垂直的判定定理得出
,再由线面垂直的判定定理得出![]() 平面
平面![]() ;(2)以O为原点,如图建立空间直角坐标系,写出各点的坐标,求出
;(2)以O为原点,如图建立空间直角坐标系,写出各点的坐标,求出![]() 的坐标,求出
的坐标,求出![]() 的值为
的值为![]() ,得出结果;(3)求出平面ABC的一个法向量,由点到平面的距离公式算出结果。
,得出结果;(3)求出平面ABC的一个法向量,由点到平面的距离公式算出结果。
试题解析:(1)连接OC,∵BO=DO,AB=AD,∴AO⊥BD,
∵BO=DO,BC=CD,∴CO⊥BD,
在△AOC中,由题设知 AO=![]() ,
, ![]() ,AC=
,AC=![]() ,
,
∴AO2+CO2=AC2, ∴∠AOC=90°,即AO⊥OC,
∵AO⊥BD,BD∩OC=O,
∴AO⊥平面BCD;
(2)以O为原点,如图建立空间直角坐标系,
则A(0,0, ![]() ),B(
),B(![]() ,0,0),C(0,
,0,0),C(0, ![]() ,0),D(﹣
,0),D(﹣![]() ,0,0),
,0,0),![]() ,
,![]() ,
, 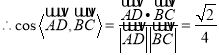 ,∴异面直线AD与BC所成角的余弦值大小为
,∴异面直线AD与BC所成角的余弦值大小为![]() .
.
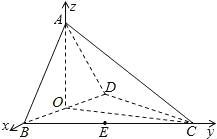
(3)解:由(2)知: ![]() ,
, ![]() .
.
设平面ABC的一个法向量为=(x,y,z),则
![]()
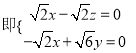 ,
,
令y=1,得![]() =(
=(![]() ,1,
,1,![]() )
)
又![]() ,
,
∴点D到平面ABC的距离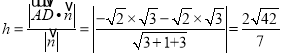 .
.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
