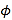题目内容
【题目】已知点![]() 是抛物线
是抛物线![]() 上一点,点
上一点,点![]() 为抛物线
为抛物线![]() 的焦点,
的焦点,![]() .
.
(1)求直线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线
与抛物线![]() 的另一个交点为
的另一个交点为![]() ,曲线
,曲线![]() 在点
在点![]() 与点
与点![]() 处的切线分别为
处的切线分别为![]() ,直线
,直线![]() 相交于点
相交于点![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据抛物线的定义,即可求得抛物线方程,以及点![]() 的坐标,利用点斜式即可求得直线方程;
的坐标,利用点斜式即可求得直线方程;
(2)联立直线![]() 的方程与抛物线方程,即可求得
的方程与抛物线方程,即可求得![]() 点坐标,求得切线
点坐标,求得切线![]() 方程,联立可得
方程,联立可得![]() 点坐标,利用点到直线距离公式和两点之间的距离公式,即可容易求得结果.
点坐标,利用点到直线距离公式和两点之间的距离公式,即可容易求得结果.
(1)因为![]() ,所以
,所以![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
又因为![]() ,且
,且![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
故直线![]() 的方程为
的方程为![]() ,化简得
,化简得![]() .
.
(2)由(1)知,抛物线![]() 的方程为
的方程为![]() ,
,
联立方程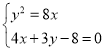 ,得
,得![]() ,
,
解得![]() 或
或![]() ,即
,即![]() ,
,
所以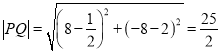 .
.
设直线![]() 的方程为
的方程为![]() ,联立
,联立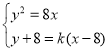 ,
,
得![]() ,由
,由![]() ,解得
,解得![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,同理可得直线
,同理可得直线![]() 的方程为
的方程为![]() ,
,
由![]() 解得
解得![]() ,即
,即![]() ,
,
设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
![]() ,
,
所以![]() 的面积为
的面积为![]() .
.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目