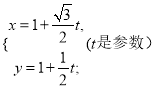题目内容
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若函数
,若函数![]() 满足:对于给定的
满足:对于给定的![]()
![]() ,存在
,存在![]() ,使得
,使得![]() 成立,那么称
成立,那么称![]() 具有性质
具有性质![]() .
.
(1)函数![]()
![]() 是否具有性质
是否具有性质![]() ?说明理由;
?说明理由;
(2)已知函数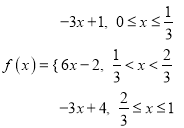 具有性质
具有性质![]() ,求
,求![]() 的最大值;
的最大值;
(3)已知函数![]() 的定义域为
的定义域为![]() ,满足
,满足![]() ,且
,且![]() 的图像是一条连续不断的曲线,问:是否存在正整数n,使得函数
的图像是一条连续不断的曲线,问:是否存在正整数n,使得函数![]() 具有性质
具有性质![]() ,若存在,求出这样的n的取值集合;若不存在,请说明理由.
,若存在,求出这样的n的取值集合;若不存在,请说明理由.
【答案】(1)不具有;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(Ⅰ)利用f(x0)=f(x0+![]() ),求出x0,根据定义,即可得出结论;
),求出x0,根据定义,即可得出结论;
(Ⅱ)m的最大值为![]() .分类进行证明,当m=
.分类进行证明,当m=![]() 时,函数f(x)具有性质P(
时,函数f(x)具有性质P(![]() );假设存在
);假设存在![]() <m<1,使得函数f(x)具有性质P(m),则0<1﹣m<
<m<1,使得函数f(x)具有性质P(m),则0<1﹣m<![]() ,证明不存在x0∈(0,1﹣m],使得f(x0)=f(x0+m)即可;
,证明不存在x0∈(0,1﹣m],使得f(x0)=f(x0+m)即可;
(Ⅲ)任取k∈N*且k≥2,设g(x)=f(x+![]() )﹣f(x),其中x∈[0,
)﹣f(x),其中x∈[0, ![]() ],利用叠加法可得g(0)+g(
],利用叠加法可得g(0)+g(![]() )+…+g(
)+…+g(![]() )+…+g(
)+…+g(![]() )=f(1)﹣f(0)=0,分类讨论:当g(0)、g(
)=f(1)﹣f(0)=0,分类讨论:当g(0)、g(![]() )、…、g(
)、…、g(![]() )中有一个为0时,函数f(x)具有性质P(
)中有一个为0时,函数f(x)具有性质P(![]() );当g(0)、g(
);当g(0)、g(![]() )、…、g(
)、…、g(![]() )均不为0时,由于其和为0,则必然存在正数和负数,进而可证函数f(x)具有性质P(
)均不为0时,由于其和为0,则必然存在正数和负数,进而可证函数f(x)具有性质P(![]() ).
).
试题解析:
(1)函数f(x)=sinx(x∈[0,1]),不具有性质P(![]() )
)
证明如下:
对任何t∈[0,1﹣![]() ]=[0,
]=[0,![]() ],均有0≤t≤t+
],均有0≤t≤t+![]() ≤1
≤1
由于函数f(x)=sinx,在x∈[0,1]上单调递增
∴f(t)<f(t+![]() )
)
所以,函数f(x)=sinx(x∈[0,1]不具有性质P(![]() )
)
(2)T的最大值为![]() .求解如下:
.求解如下:
∵f(![]()
![]() )=f(1)=﹣3×1﹣4=1,又f(
)=f(1)=﹣3×1﹣4=1,又f(![]() )=6×
)=6×![]() ﹣2=1
﹣2=1
∴f(t+![]() )=f(t)在t∈[0,1﹣
)=f(t)在t∈[0,1﹣![]() ]上有解,t=
]上有解,t=![]()
因此,f(x)具有性质P(![]() ),从而T可取到
),从而T可取到![]()
下证: ![]() <T<1不可能出现.
<T<1不可能出现.
首先,当x∈(0, ![]() ]时,f(x)=﹣3x+1<1,当x∈(
]时,f(x)=﹣3x+1<1,当x∈(![]() ,
, ![]() )时,f(x)=6x﹣2<6×
)时,f(x)=6x﹣2<6×![]() ﹣2=1
﹣2=1
即,当x∈(0, ![]() )时,均有f(x)<1,同理可得,当x∈(
)时,均有f(x)<1,同理可得,当x∈(![]() ,1),均有f(x)>1.
,1),均有f(x)>1.
假设![]() <T<1,那么,当t∈
<T<1,那么,当t∈
①若t=0,则f(t)=f(0)=1,又t+T=T∈(![]() ,1),
,1),
所以f(t+T)=f(T)>1,即f(t+T)>f(t)
②若t∈(0,1﹣T] ![]() (0,
(0, ![]() ),则f(t)<1,又t+T∈(T,1),注意到
),则f(t)<1,又t+T∈(T,1),注意到![]() <T<1,故
<T<1,故
f(t+T)>1,故f(t+T)>f(t)
这就是说,如果![]() <T<1,那么,当t∈[0,1﹣T]时,
<T<1,那么,当t∈[0,1﹣T]时,
均有f(t+T)>f(t),即f(t+T)=f(t)均不成立
综上所述,T的最大值为![]()
(3)任取n∈N+,n≥2,设h(x)=f(x+![]() )﹣f(x),其中x∈[0,
)﹣f(x),其中x∈[0,![]() ],则有
],则有
h(0)=f(![]() )﹣f(0)
)﹣f(0)
h(![]() )=f(
)=f(![]() )﹣f(
)﹣f(![]() )
)
h(![]() )=f(
)=f(![]() )﹣f(
)﹣f(![]() )
)
…
h(![]() )=f(
)=f(![]() )﹣f(
)﹣f(![]() )
)
…
h(![]() )=f(1)﹣f(
)=f(1)﹣f(![]() )
)
以上各式相加得h(0)+h(![]() )+f(
)+f(![]() )+…+h(
)+…+h(![]() )+…+h(
)+…+h(![]() )=f(1)﹣f(0)=0,
)=f(1)﹣f(0)=0,
即h(0)+h(![]() )+f(
)+f(![]() )+…+h(
)+…+h(![]() )+…+h(
)+…+h(![]() )=0
)=0
当h(0),h(![]() ),f(
),f(![]() ),…,h(
),…,h(![]() )中有一个为0时,不妨设为h(
)中有一个为0时,不妨设为h(![]() )=0,这里i∈{0,1,2,…,n﹣1},
)=0,这里i∈{0,1,2,…,n﹣1},
而0=h(![]() )=f(
)=f(![]() +
+![]() )﹣f(
)﹣f(![]() ),即f(
),即f(![]() +
+![]() )﹣f(
)﹣f(![]() )=0
)=0
推得f(![]() +
+![]() )=f(
)=f(![]() )
)
故函数f(x)具有性质P(![]() )(n∈N+,n≥2)
)(n∈N+,n≥2)
当h(0),h(![]() ),f(
),f(![]() ),…,h(
),…,h(![]() )均不为0时,因为其和为0,所以必然存在正数与负数,
)均不为0时,因为其和为0,所以必然存在正数与负数,
不妨设h(![]() )>0,h(
)>0,h(![]() )<0,(i<j,i,j∈{0,1,2…,n﹣1})
)<0,(i<j,i,j∈{0,1,2…,n﹣1})
由于h(x)的图象也是连续不断的曲线,故,至少存在一个t∈(![]() ,
,![]() )使得h(t)=0,即f(t+
)使得h(t)=0,即f(t+![]() )﹣f(t)=0.
)﹣f(t)=0.
亦即f(t+![]() )=f(t),故函数f(x)具有性质P(
)=f(t),故函数f(x)具有性质P(![]() )(n∈N+,n≥2)
)(n∈N+,n≥2)
综上所述,存在正整数n,且n的取值集合是{n|n∈N+,n≥2}.

【题目】某地区2010年至2016年农村居民家庭纯收入![]() (单位:千元)的数据如下表
(单位:千元)的数据如下表
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求![]() 关于
关于![]() 的线性回归方程。
的线性回归方程。
(2)判断![]() 与
与![]() 之间是正相关还是负相关?
之间是正相关还是负相关?
(3)预测该地区2018年农村居民家庭人均纯收入。
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
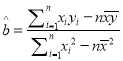 ,
, ![]()