题目内容
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点O为极点, ![]() 轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知过点P(1,1)的直线
轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知过点P(1,1)的直线![]() 的参数方程是
的参数方程是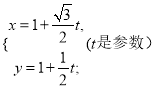
(I)写出直线![]() 的极坐标方程;
的极坐标方程;
(II)设![]() 与圆
与圆![]() 相交于两点A、B,求点P到A、B两点的距离之积
相交于两点A、B,求点P到A、B两点的距离之积
【答案】(I)![]() ;(Ⅱ)2.
;(Ⅱ)2.
【解析】试题分析:(I)消去参数t得到直线的普通方程,利用极直互化得到极坐标方程;;
(II)将圆![]() 化成普通方程,再与直线的参数方程联解,得到一个关于t的一元二次方程.再用一元二次方程根与系数的关系,结合两点的距离公式,可得出P到A、B两点的距离之积.
化成普通方程,再与直线的参数方程联解,得到一个关于t的一元二次方程.再用一元二次方程根与系数的关系,结合两点的距离公式,可得出P到A、B两点的距离之积.
试题解析:
(I)因为直线的参数方程是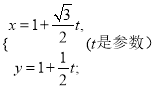 .所以直线
.所以直线![]() 的普通方程是
的普通方程是![]() 。化为极坐标方程为
。化为极坐标方程为![]() .
.
(II)因为点A,B都在直线l上,所以可设它们对应的参数为t1和t2,则点A,B的坐标分别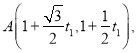
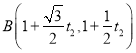 .
.
圆![]() 化为直角坐标系的方程
化为直角坐标系的方程![]() .
.
以直线![]() 的参数方程代入圆的方程
的参数方程代入圆的方程![]() 整理得到
整理得到
![]() ①
①
因为![]() 和
和![]() 是方程①的解,从而
是方程①的解,从而![]() =-2.
=-2.
所以|PA|·|PB|= |![]() |=|-2|=2.
|=|-2|=2.

练习册系列答案
相关题目
【题目】某小学为了解本校某年级女生的身高情况,从本校该年级的学生中随机选出100名女生并统计她们的身高(单位: ![]() ),得到如图频率分布表:
),得到如图频率分布表:
分组(身高) |
|
|
|
|
(Ⅰ)用分层抽样的方法从身高在![]() 和
和![]() 的女生中共抽取6人,则身高在
的女生中共抽取6人,则身高在![]() 的女生应抽取几人?
的女生应抽取几人?
(Ⅱ)在(Ⅰ)中抽取的6人中,再随机抽取2人,求这2人身高都在![]() 内的概率.
内的概率.