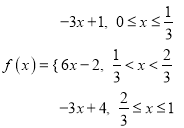题目内容
【题目】设函数f(x)=sin(2ωx+ ![]() )(其中ω>0),且f(x)的图象在y轴右侧的第一个最高点的横坐标是
)(其中ω>0),且f(x)的图象在y轴右侧的第一个最高点的横坐标是 ![]() .
.
(1)求y=f(x)的最小正周期及对称轴;
(2)若x∈ ![]() ,函数
,函数 ![]() ﹣af(x)+1的最小值为0.求a的值.
﹣af(x)+1的最小值为0.求a的值.
【答案】
(1)解:由题意,根据五点法作图可得2ω ![]() +
+ ![]() =
= ![]() ,求得ω=
,求得ω= ![]() ;
;
所以函数y=f(x)=sin(x+ ![]() )的最小正周期是T=2π;
)的最小正周期是T=2π;
令x+ ![]() =
= ![]() +kπ,k∈Z,
+kπ,k∈Z,
解得x= ![]() +kπ,k∈Z,
+kπ,k∈Z,
所以函数y=f(x)的对称轴是x= ![]() +kπ,k∈Z
+kπ,k∈Z
(2)解:由(1)可得函数f(x)=sin(x+ ![]() ),
),
在区间[﹣ ![]() ,
, ![]() ]上,x+
]上,x+ ![]() ∈[0,
∈[0, ![]() ],
],
所以f(x)=sin(x+ ![]() )∈[﹣
)∈[﹣ ![]() ,1];
,1];
所以g(x)=sin2[(x+ ![]() )+
)+ ![]() ]﹣asin(x+
]﹣asin(x+ ![]() )+1
)+1
=1﹣sin2(x+ ![]() )﹣asin(x+
)﹣asin(x+ ![]() )+1
)+1
=﹣ ![]() +2+
+2+ ![]() ;
;
当﹣ ![]() ≤﹣
≤﹣ ![]() ≤1时,﹣2≤a≤1,函数g(x)的最小值是g(x)min=2+
≤1时,﹣2≤a≤1,函数g(x)的最小值是g(x)min=2+ ![]() =0,无解;
=0,无解;
当﹣ ![]() <﹣
<﹣ ![]() 时,a>1,函数g(x)的最小值是g(x)min=2﹣
时,a>1,函数g(x)的最小值是g(x)min=2﹣ ![]() ﹣a=0,解得a=
﹣a=0,解得a= ![]() ;
;
当﹣ ![]() >1时,a<﹣2,函数g(x)的最小值是g(x)min=2﹣1﹣a=0,解得a=1(不合题意,舍去);
>1时,a<﹣2,函数g(x)的最小值是g(x)min=2﹣1﹣a=0,解得a=1(不合题意,舍去);
综上,函数g(x)取得最小值0时,a= ![]()
【解析】(1)由题意,根据五点法作图求出ω的值,即可求函数y=f(x)的最小正周期;写出函数y=f(x)的解析式,即可求出它的对称轴;(2)求出函数f(x)在区间[﹣ ![]() ,
, ![]() ]上的取值范围,再化简函数g(x),讨论a的取值,求出函数g(x)取最小值0时a的值.
]上的取值范围,再化简函数g(x),讨论a的取值,求出函数g(x)取最小值0时a的值.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案【题目】为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:( )
做不到“光盘” | 能做到“光盘” | |
男 | 45 | 10 |
女 | 30 | 15 |
附:
P(K2 | 0.10 | 0.05 | 0.025 |
k | 2.706 | 3.841 | 5.024 |
![]()
参照附表,得到的正确结论是
A.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别无关”
C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”
【题目】某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为
,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为![]() .
.
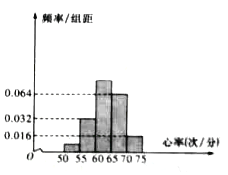
(Ⅰ)求![]() 的值,并求这50名同学心率的平均值;
的值,并求这50名同学心率的平均值;
(Ⅱ)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为0.8,请将下面的列联表补充完整,并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关?说明你的理由.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: 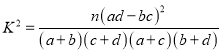 ,其中
,其中![]()
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计 | 50 |