Question

【题目】已知二次函数的图象如图所示．
（1）写出该函数的零点；
（2）写出该函数的解析式．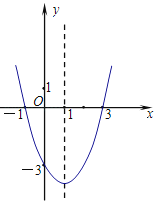

Answer 1

【答案】解：（1）由图象可知抛物线的与x轴的交点坐标是（﹣1，0），（3，0），
即当x=﹣1或3时，y=0
故该函数函数的零点是﹣1，3；
（2）设二次函数的解析式为y=a（x+1）（x﹣3）（a≠0），
将点（0，﹣3）代入代入解析式得：a（0+1）（0﹣3）=﹣3
解之得：a=1（6分）
∴函数的解析式是y=x2﹣2x﹣3．
【解析】（1）由图象可知抛物线的与x轴的交点坐标是（﹣1，0），（3，0），再结合零点的定义写出该函数的零点即可；
（2）由（1）可设抛物线解析式的交点式y=a（x+1）（x﹣3）（a≠0），再将点（0，﹣3）代入求a即可．
【考点精析】本题主要考查了二次函数的图象的相关知识点，需要掌握二次函数的图象是一条抛物线，对称轴方程为顶点坐标是才能正确解答此题．