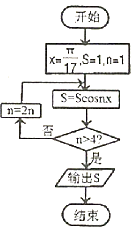
题目内容
【题目】本题满分14分)
在数列![]() 中,
中,![]() ,且
,且![]() .
.
(Ⅰ) 求![]() ,猜想
,猜想![]() 的表达式,并加以证明;
的表达式,并加以证明;
(Ⅱ) 设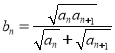 ,求证:对任意的自然数
,求证:对任意的自然数![]() ,都有
,都有![]() ;
;
【答案】
解:(1)容易求得:![]() ,
,![]() ;
;
猜想![]() ,
,![]() 证明:见解析.
证明:见解析.
(2)见解析.
【解析】本试题主要是考查了数列的归纳猜想的思想的运用,以及运用哦递推关系式来求解数列的前几项,并且能运用数学归纳法加以证明,同时对于构造的新数列也能利用裂项法求和的综合运用。
(1)利用递推关系,对于n赋值分别得到前几项,并猜想其通项公式,运用数学归纳法加以证明
(2)根据上一问的结论,表示新数列的通项公式,然后利用裂项的思想求和并证明不等式问题。
解:(1)容易求得:![]() ,
,![]() ----------------------(2分)
----------------------(2分)
故可以猜想![]() ,
,![]() 下面利用数学归纳法加以证明:
下面利用数学归纳法加以证明:
显然当![]() 时,结论成立,-----------------(3分)
时,结论成立,-----------------(3分)
假设当![]() ;
;![]() 时(也可以
时(也可以![]() ),结论也成立,即
),结论也成立,即
![]() ,
,![]() --------------------------(4分)
--------------------------(4分)
那么当![]() 时,由题设与归纳假设可知:
时,由题设与归纳假设可知:
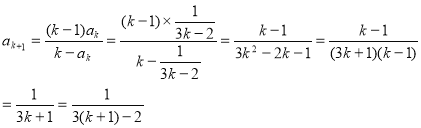 ------------(6分)
------------(6分)
即当![]() 时,结论也成立,综上,对
时,结论也成立,综上,对![]() ,
,![]() 成立。--------(7分)
成立。--------(7分)
(2) ---(9分)
---(9分)
所以
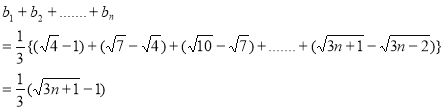 ---------(11分)
---------(11分)
所以只需要证明![]()
![]()
![]()
![]()
![]()
![]()
![]() (显然成立)
(显然成立)
所以对任意的自然数![]() ,都有
,都有![]() -------(14分)
-------(14分)

 阅读快车系列答案
阅读快车系列答案【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
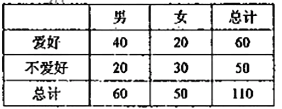
由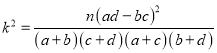 算得,
算得, ![]() .
.
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
则参照附表,得到的正确结论应是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C. 有99%以上的把握认为“爱好该项运动与性别有关”
D. 有99%以上的把握认为“爱好该项运动与性别无关”