题目内容
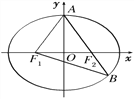
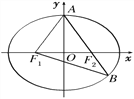
【题目】如图,F1,F2分别是椭圆![]() 的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
(Ⅰ)求椭圆C的离心率;
(Ⅱ)已知△AF1B的面积为![]() ,求椭圆C的方程.
,求椭圆C的方程.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]()
【解析】试题分析 :(Ⅰ)由题意可知![]() 为等边三角形
为等边三角形![]() ;
;
(Ⅱ)法一:先求AB的方程为![]() ,代入椭圆方程解得
,代入椭圆方程解得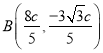
![]() .
.
试题解析:(Ⅰ)由题意可知,△AF1F2为等边三角形,a=2c,所以e=![]() =
=![]() .
.
(Ⅱ)法一:a2=4c2,b2=3c2,直线AB的方程为y=-![]() (x-c).
(x-c).
将其代入椭圆方程3x2+4y2=12c2,
得B![]() .又A(0,
.又A(0,![]() c),所以|AB|=
c),所以|AB|=![]() =
=![]() c.
c.
由S△AF1B=![]() |AF1|·|AB|sin ∠F1AB=
|AF1|·|AB|sin ∠F1AB=![]() a·
a·![]() c·
c·![]() =
=![]() a2=40
a2=40![]() ,解得a=10,c=5,
,解得a=10,c=5,
则b2=75,即b=5![]() .所以椭圆C的方程为:
.所以椭圆C的方程为:![]() +
+![]() =1. …………4分
=1. …………4分
法二:设|AB|=t.因为|AF2|=a,所以|BF2|=t-a.
由椭圆定义|BF1|+|BF2|=2a,可知|BF1|=3a-t.
再由余弦定理(3a-t)2=a2+t2-2atcos 60°,可得t=![]() a.
a.
由S△AF1B=![]() |AF1|·|AB|·sin∠F1AB=
|AF1|·|AB|·sin∠F1AB=![]() a·
a·![]() a·
a·![]() =
=![]() a2=40
a2=40![]() ,
,
解得a=10,则c=5,b=5![]() .所以椭圆C的方程为:
.所以椭圆C的方程为:![]() +
+![]() =1. ………………10分
=1. ………………10分

【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |