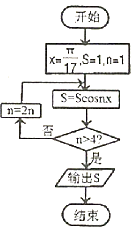
题目内容
【题目】已知函数f(x)=﹣x3+ax2+bx+c图像上的点P(1,f(1))处的切线方程为y=﹣3x+1.
(1)若函数f(x)在x=﹣2时有极值,求f(x)的表达式;
(2)函数f(x)在区间[﹣2,0]上单调递增,求实数b的取值范围.
【答案】
(1)解:f′(x)=﹣3x2+2ax+b,
函数f(x)在x=1处的切线斜率为﹣3,
∴f′(1)=﹣3+2a+b=﹣3,即2a+b=0,
又f(1)=﹣1+a+b+c=﹣2得a+b+c=﹣1.
∵函数f(x)在x=﹣2时有极值,
∴f′(﹣2)=﹣12﹣4a+b=0,
联立 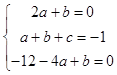 ,
,
解得a=﹣2,b=4,c=﹣3,
∴f(x)=﹣x3﹣2x2+4x﹣3
(2)解:∵函数f(x)在区间[﹣2,0]上单调递增,
∴导函数f′(x)=﹣3x2﹣bx+b在区间[﹣2,0]上的值恒大于或等于零,
则 ![]() ,
,
解得b≥4,
∴实数b的取值范围为[4,+∞)
【解析】(1)f′(x)=﹣3x2+2ax+b,由函数f(x)在x=1处的切线斜率为﹣3,可得f′(1)=﹣3;又f(1)=﹣1+a+b+c=﹣2;由函数f(x)在x=﹣2时有极值,可得f′(﹣2)=0,联立解得即可.(2)由于函数f(x)在区间[﹣2,0]上单调递增,可得导函数f′(x)=﹣3x2﹣bx+b在区间[﹣2,0]上的值恒大于或等于零,因此 ![]() ,解得即可.
,解得即可.
【考点精析】根据题目的已知条件,利用函数的极值与导数的相关知识可以得到问题的答案,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
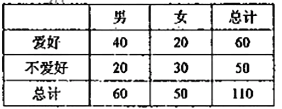
由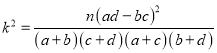 算得,
算得, ![]() .
.
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
则参照附表,得到的正确结论应是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C. 有99%以上的把握认为“爱好该项运动与性别有关”
D. 有99%以上的把握认为“爱好该项运动与性别无关”