题目内容
(本小题满分12分)
已知函数f (x )=ln(1+x)+a (x+1)2(a为常数).
)=ln(1+x)+a (x+1)2(a为常数).
(Ⅰ)若函数f (x)在x=1处有极值,判断该极值是极大值还是极小值;
(Ⅱ)对满足条件a≤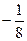 的任意一个a,方程f (x)=0在区间(0,3)内实数根的个数是多少?
的任意一个a,方程f (x)=0在区间(0,3)内实数根的个数是多少?
已知函数f (x
 )=ln(1+x)+a (x+1)2(a为常数).
)=ln(1+x)+a (x+1)2(a为常数).(Ⅰ)若函数f (x)在x=1处有极值,判断该极值是极大值还是极小值;

(Ⅱ)对满足条件a≤
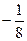 的任意一个a,方程f (x)=0在区间(0,3)内实数根的个数是多少?
的任意一个a,方程f (x)=0在区间(0,3)内实数根的个数是多少? (1)极大值;(2)2
(Ⅰ)f'(x)=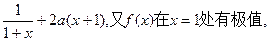
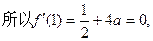
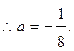 …………2分
…………2分
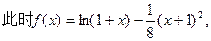
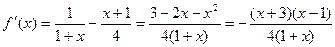
—1<x<1时,f'(x)>0;x>1时,f'(x)<0,
∴f(x)在(—1,1)上为增函数,在(1,+∞)上为减函数
所以f(1)为函数f(x)的极大值 …………4分
(Ⅱ)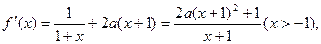
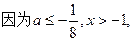
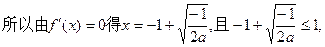 …………5分
…………5分
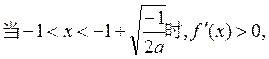
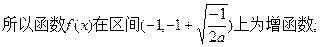
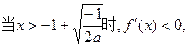
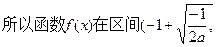 +∞)是为减函数
+∞)是为减函数
因此f(x)在x=—1+ 处取得区间(—1,+∞)上的最大值 ——6分
处取得区间(—1,+∞)上的最大值 ——6分
由f(—1+ )=0得a=—
)=0得a=—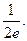 …………7分
…………7分
(1)当a<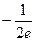 时,f(—1+
时,f(—1+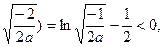
所以方程f(x)=0在区间(0,3)内无实数根 …………8分
(2)当a=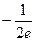 时,f(—1+
时,f(—1+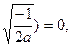
所以方程f(x)=0在区间(0,3)内有且仅有1个实数根
—1+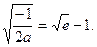 …………9分
…………9分
(3)当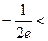 a≤
a≤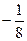 时,
时,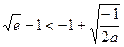 ≤1,
≤1,
又f(0)a<0,f(—1+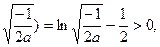
f(3)=ln4+16a≤ln4-2<0,
所以方程f(x)=0在区间(0,3)内有2个实数根. …………11分
综上所述,
当a<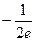 时,方程f(x)=0在区间(0,3)内无实数根;
时,方程f(x)=0在区间(0,3)内无实数根;
当a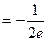 时,方程f(x)=0在区间(0,3)内有1个实数根;
时,方程f(x)=0在区间(0,3)内有1个实数根;
当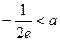 ≤
≤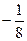 时,方程f(x)=0 在区间(0,3),内有2个实数根.
时,方程f(x)=0 在区间(0,3),内有2个实数根.
…………12分
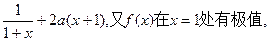
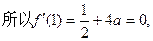
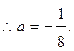 …………2分
…………2分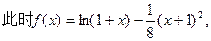
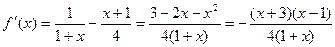
—1<x<1时,f'(x)>0;x>1时,f'(x)<0,
∴f(x)在(—1,1)上为增函数,在(1,+∞)上为减函数
所以f(1)为函数f(x)的极大值 …………4分
(Ⅱ)
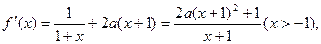
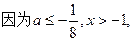
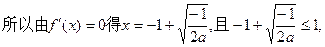 …………5分
…………5分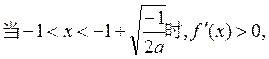
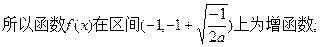
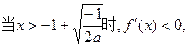
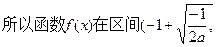 +∞)是为减函数
+∞)是为减函数因此f(x)在x=—1+
 处取得区间(—1,+∞)上的最大值 ——6分
处取得区间(—1,+∞)上的最大值 ——6分由f(—1+
 )=0得a=—
)=0得a=—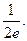 …………7分
…………7分(1)当a<
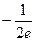 时,f(—1+
时,f(—1+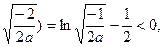
所以方程f(x)=0在区间(0,3)内无实数根 …………8分
(2)当a=
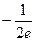 时,f(—1+
时,f(—1+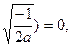
所以方程f(x)=0在区间(0,3)内有且仅有1个实数根
—1+
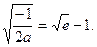 …………9分
…………9分(3)当
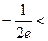 a≤
a≤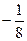 时,
时,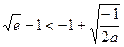 ≤1,
≤1,又f(0)a<0,f(—1+
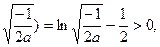
f(3)=ln4+16a≤ln4-2<0,
所以方程f(x)=0在区间(0,3)内有2个实数根. …………11分
综上所述,
当a<
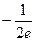 时,方程f(x)=0在区间(0,3)内无实数根;
时,方程f(x)=0在区间(0,3)内无实数根;当a
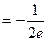 时,方程f(x)=0在区间(0,3)内有1个实数根;
时,方程f(x)=0在区间(0,3)内有1个实数根;当
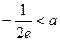 ≤
≤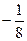 时,方程f(x)=0 在区间(0,3),内有2个实数根.
时,方程f(x)=0 在区间(0,3),内有2个实数根.…………12分

练习册系列答案
相关题目
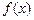 满足
满足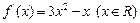 ,试写出一个符合题意的函数
,试写出一个符合题意的函数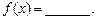
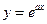 在点
在点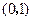 处的切线与直线
处的切线与直线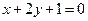 垂直,则
垂直,则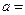 。
。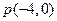 作曲线
作曲线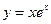 的切线,则切线方程为 。
的切线,则切线方程为 。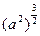 =a3 ,②
=a3 ,②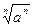 =|a| ,③函数y=
=|a| ,③函数y=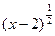 -(3x-7)0的定义域是(2, +∞), ④若
-(3x-7)0的定义域是(2, +∞), ④若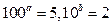 ,则2a+b=1其中正确的个数是
,则2a+b=1其中正确的个数是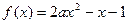 在区间(0,1)内恰有一个零点,则实数a的取值范围是( )
在区间(0,1)内恰有一个零点,则实数a的取值范围是( ) 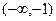
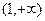
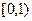
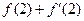 的值是 ( )
的值是 ( )
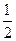
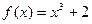 ,则过点P(1,3)的切线方程为_________________________.
,则过点P(1,3)的切线方程为_________________________.