题目内容
已知函数f(x)=
,若方程f(x)-kx+k=0有两个实数根,则k的取值范围是( )
|
A.(-1,-
| B.[-
| C.[-1,+∞) | D.[-
|
当0≤x<1时,-1≤x-1<0,
所以f(x)=
-1=
-1,
由f(x)-kx+k=0得f(x)=kx-k,分别作出y=f(x)和y=kx-k=k(x-1)的图象,如图: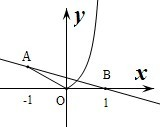
由图象可知当直线y=kx-k经过点A(-1,1)时,两曲线有两个交点,又直线y=k(x-1)过定点B(1,0),
所以过A,B两点的直线斜率k=-
.
所以要使方程f(x)-kx+k=0有两个实数根,
则-
≤k<0.
故选B.
所以f(x)=
| 1 |
| f(x-1) |
| 1 |
| -(x-1) |
由f(x)-kx+k=0得f(x)=kx-k,分别作出y=f(x)和y=kx-k=k(x-1)的图象,如图:

由图象可知当直线y=kx-k经过点A(-1,1)时,两曲线有两个交点,又直线y=k(x-1)过定点B(1,0),
所以过A,B两点的直线斜率k=-
| 1 |
| 2 |
所以要使方程f(x)-kx+k=0有两个实数根,
则-
| 1 |
| 2 |
故选B.

练习册系列答案
相关题目