题目内容
设函数f(x)=x2-2|x|-3(-3≤x≤3),
(1)证明函数f(x)是偶函数;
(2)用分段函数表示f(x)并作出其图象;
(3)指出函数f(x)的单调区间及相应的单调性;
(4)求函数的值域.
(1)证明函数f(x)是偶函数;
(2)用分段函数表示f(x)并作出其图象;
(3)指出函数f(x)的单调区间及相应的单调性;
(4)求函数的值域.

(1)∵-3≤x≤3,
∴函数的定义域关于原点对称,
又∵f(-x)=(-x)2-2|-x|-3=x2-2|x|-3=f(x)
∴函数f(x)是偶函数.
(2)f(x)=
;
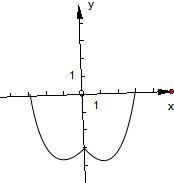
(3)由(2)中图象可得:
函数f(x)的单调增区间是[-1,0],[1,3];
函数f(x)的单调减区间是[-3,-1],[0,1].
(4)由(2)中图象可得:
函数的值域是[-4,0].
∴函数的定义域关于原点对称,
又∵f(-x)=(-x)2-2|-x|-3=x2-2|x|-3=f(x)
∴函数f(x)是偶函数.
(2)f(x)=
|
(3)由(2)中图象可得:
函数f(x)的单调增区间是[-1,0],[1,3];
函数f(x)的单调减区间是[-3,-1],[0,1].
(4)由(2)中图象可得:
函数的值域是[-4,0].


练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目










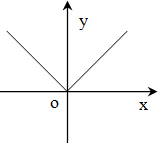
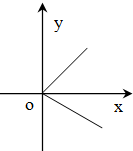
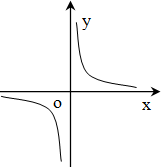
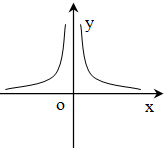






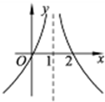

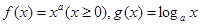 的图像可能是( )
的图像可能是( )