题目内容
设f(x)=
,若存在互异的三个实数x1,x2,x3,使f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围是( )
|
| A.(3,4) | B.(2,5) | C.(1,2) | D.(3,5) |
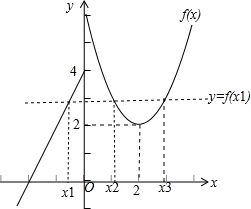
设实数x1 <x2 <x3 ,画出函数f(x)的图象,如图所示:由f(x1)>2 可得-1<x1<0.
再由二次函数的性质可得 x2+x3 =4,∴3<x1+x2+x3 <4,
故选A.
再由二次函数的性质可得 x2+x3 =4,∴3<x1+x2+x3 <4,
故选A.


练习册系列答案
相关题目

