题目内容
19．如图，在三棱锥P-ABC中，平面PAB⊥平面ABC，PA=PB=PC，M、N分别为AB、BC的中点．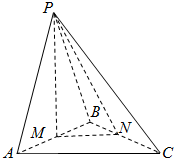
（1）求证：AC∥平面PMN；
（2）求证：MN⊥BC．
分析 （1）由已知可证MN∥AC，根据直线与平面平行的判定定理即可证明AC∥平面PMN．
（2）易证明PM⊥AB，PN⊥BC，由平面PAB⊥平面ABC，可证PM⊥BC，从而证明BC⊥平面PMN，MN?平面PMN，即可得证．
解答 证明：（1）因为M、N分别为AB、BC的中点，所以MN∥AC…（3分）
又因为MN?平面PMN，AC?平面PMN，所以AC∥平面PMN…（7分）
（2）因为PA=PB=PC，M、N分别为AB、BC的中点，
所以PM⊥AB，PN⊥BC，
又因为平面PAB⊥平面ABC，PM?平面PAB，平面PAB∩平面ABC=AB，
所以PM⊥平面ABC…（10分）
又BC?平面ABC，
所以PM⊥BC，
所以BC⊥平面PMN，
因为MN?平面PMN，
所以MN⊥BC…（14分）
点评 本题主要考查了直线与平面平行的判定，直线与平面垂直的性质，考查了空间想象能力和推理论证能力，属于中档题．
练习册系列答案
相关题目
10．已知向量$\overrightarrow a=（1，2）$，$\overrightarrow b=（3，1）$，则$\overrightarrow b-\overrightarrow a$=（ ）
| A． | （2，-1） | B． | （-2，1） | C． | （2，0） | D． | （4，3） |
4．某12人的兴趣小组中，有5名“三好生”，现从小组中任意选6人参加竞赛，用ξ表示这6人中“三好生”的人数，则下列概率中等于$\frac{{C}_{5}^{3}{C}_{7}^{3}}{{C}_{12}^{6}}$的是（ ）
| A． | P（ξ=2） | B． | P（ξ=3） | C． | P（ξ≤2） | D． | P（ξ≤3） |
11．已知函数y=ax3-x在（-1，1）上是单调减函数，则实数a的取值范围（ ）
| A． | a＜$\frac{1}{3}$ | B． | a=1 | C． | a=$\frac{1}{3}$ | D． | a≤$\frac{1}{3}$ |
