题目内容
6.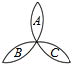 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示,假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是$\frac{1}{3}$.
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示,假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是$\frac{1}{3}$.
分析 根据条件先求出逆时针和顺时针跳的概率,然后根据跳3次回到A,则应满足3次逆时针或者3次顺时针,根据概率公式即可得到结论
解答 解:设按照顺时针跳的概率为p,则逆时针方向跳的概率为2p,则p+2p=3p=1,
解得p=$\frac{1}{3}$,即按照顺时针跳的概率为$\frac{1}{3}$,则逆时针方向跳的概率为$\frac{2}{3}$,
若青蛙在A叶上,则跳3次之后停在A叶上,
则满足3次逆时针或者3次顺时针,
①若先按逆时针开始从A→B,则对应的概率为$\frac{2}{3}×\frac{2}{3}×\frac{2}{3}$=$\frac{8}{27}$,
②若先按顺时针开始从A→C,则对应的概率为=$\frac{1}{3}$×$\frac{1}{3}$×$\frac{1}{3}$=$\frac{1}{27}$,
则概率为$\frac{8}{27}$+$\frac{1}{27}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$
点评 本题主要考查概率的计算,利用独立重复试验的概率公式是解决本题的关键.

练习册系列答案
相关题目
11.已知函数y=ax3-x在(-1,1)上是单调减函数,则实数a的取值范围( )
| A. | a<$\frac{1}{3}$ | B. | a=1 | C. | a=$\frac{1}{3}$ | D. | a≤$\frac{1}{3}$ |
18.在曲线y=x3上切线的斜率为3的点是( )
| A. | (0,0) | B. | (1,1) | C. | (-1,-1) | D. | (1,1)或(-1,-1) |
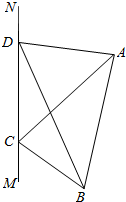 如图,为对某失事客轮AB进行有效援助,现分别在河岸MN选择两处C、D用强光柱进行辅助照明,其中A、B、C、D在同一平面内.现测得CD长为100米,∠ADN=105°,∠BDM=30°,∠ACN=45°,∠BCM=60°.
如图,为对某失事客轮AB进行有效援助,现分别在河岸MN选择两处C、D用强光柱进行辅助照明,其中A、B、C、D在同一平面内.现测得CD长为100米,∠ADN=105°,∠BDM=30°,∠ACN=45°,∠BCM=60°.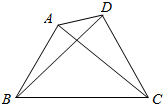 在四边形ABCD中,AB=$\sqrt{3}$,CD=2,∠BAD=135°,∠BCD=60°,∠ADB=30°.
在四边形ABCD中,AB=$\sqrt{3}$,CD=2,∠BAD=135°,∠BCD=60°,∠ADB=30°.