题目内容
设x0是函数f(x)=x2+log2x的零点,若有0<a<x0,则f(a)的值满足( )
| A.f(a)=0 | B.f(a)>0 |
| C.f(a)<0 | D.f(a)的符号不确定 |
由f(x)=x2+log2x=0得log2x=-x2,设函数y=log2x,y=-x2,
在同一坐标系中分别作出两个函数的图象如图:
由图象可知当0<a<x0时,log2a<-a2,即log2a+a2<0,
所以f(a)=a2+log2a<0.
故选C.
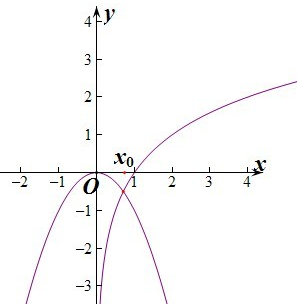
在同一坐标系中分别作出两个函数的图象如图:
由图象可知当0<a<x0时,log2a<-a2,即log2a+a2<0,
所以f(a)=a2+log2a<0.
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目