题目内容
5.已知函数f(x)=x2+3x|x-c|,其中c∈R.(1)当$c=\frac{1}{3}$时,是否存在区间[a,b],使得函数f(x)的定义域与值域均为[a,b]?若存在,求出所有可能的区间[a,b],若不存在请说明理由.
(2)若c>0,函数f(x)在区间(a,b)上既有最大值又有最小值,请分别求出a,b的取值范围(用c表示).
分析 (1)求出f(x)的分段函数,对a,b讨论,当a<b$≤\frac{1}{4}$时,当a$≤\frac{1}{4}$<$\frac{1}{3}$≤b时,当$\frac{1}{4}$$≤a≤b≤\frac{1}{3}$时,当$\frac{1}{4}$≤a≤$\frac{1}{3}$<b时,当$\frac{1}{3}$≤a<b时,运用单调性,得到方程,解得可得所求区间;
(2)画出函数的图象,要使得函数f(x)在开区间(a,b)内既有最大值又有最小值,则最小值一定在x=c处取得,最大值在$x=\frac{3}{4}c$处取得,分别求得函数值为c2时,x=$\frac{1}{2}$c,函数值为$\frac{9}{8}$c2时,x=$\frac{3+\sqrt{3}}{8}$c,即可得到a,b的范围.
解答  解:f(x)=$\left\{\begin{array}{l}{4{x}^{2}-3cx,x≥c}\\{-2{x}^{2}+3cx,x<c}\end{array}\right.$.
解:f(x)=$\left\{\begin{array}{l}{4{x}^{2}-3cx,x≥c}\\{-2{x}^{2}+3cx,x<c}\end{array}\right.$.
(1)当c=$\frac{1}{3}$时,f(x)=$\left\{\begin{array}{l}{4{x}^{2}-x,x≥\frac{1}{3}}\\{-2{x}^{2}+x,x<\frac{1}{3}}\end{array}\right.$,
当a<b$≤\frac{1}{4}$时,f(x)在区间[a,b]上单调递增,
所以$\left\{\begin{array}{l}{f(a)=a}\\{f(b)=b}\end{array}\right.$即为$\left\{\begin{array}{l}{-2{a}^{2}+a=a}\\{-2{b}^{2}+b=b}\end{array}\right.$,
所以a=b矛盾;当a$≤\frac{1}{4}$$≤b<\frac{1}{3}$时,b=f($\frac{1}{4}$)=$\frac{1}{8}$,矛盾;
当a$≤\frac{1}{4}$<$\frac{1}{3}$≤b时,b$≥\frac{1}{3}>\frac{1}{8}$>f(a),
故f(x)在区间[a,b]上的最大值在区间[$\frac{1}{3}$,b]上取得.
f(x)在[$\frac{1}{3}$,b]上单调递增,则b=f(b),
即4b2-b=b,解得b=$\frac{1}{2}$.
又a$≤\frac{1}{4}$,且a$≤\frac{1}{9}$,所以f(x)在区间[a,b]上最小值在区间[a,$\frac{1}{4}$]上取得,
又f(x)在区间[a,$\frac{1}{4}$]上单调递增,故a=f(a),即-2a2+a=a,解得a=0,
故[a,b]=[0,$\frac{1}{2}$].
当$\frac{1}{4}$$≤a≤b≤\frac{1}{3}$时,由x∈[$\frac{1}{4}$,$\frac{1}{3}$],得$\frac{1}{9}$$≤f(x)≤\frac{1}{8}$,则$\frac{1}{9}$≤a<b≤$\frac{1}{8}$矛盾.
当$\frac{1}{4}$≤a≤$\frac{1}{3}$<b时,f(x)在区间[$\frac{1}{4}$,$\frac{1}{3}$]上单调递减,在[$\frac{1}{3}$,b]上单调递增.
故a=f($\frac{1}{3}$)=$\frac{1}{9}$,矛盾.
当$\frac{1}{3}$≤a<b时,f(x)在区间[a,b]上单调递增,故$\left\{\begin{array}{l}{f(a)=a}\\{f(b)=b}\end{array}\right.$,得a=b=$\frac{1}{2}$,矛盾.
综上所述$\left\{\begin{array}{l}{a=0}\\{b=\frac{1}{2}}\end{array}\right.$,即存在区间[0,$\frac{1}{2}$]满足条件.
(2)当c>0时,函数的图象如图,
要使得函数f(x)在开区间(a,b)内既有最大值又有最小值,
则最小值一定在x=c处取得,
最大值在$x=\frac{3}{4}c$处取得,f(c)=c2,
在区间(-∞,c)内,函数值为c2时,x=$\frac{1}{2}$c,
所以$\frac{1}{2}$c≤a<$\frac{3}{4}$c;
f($\frac{3}{4}$c)=$\frac{9}{8}$c2,而在区间(a,+∞)内函数值为$\frac{9}{8}$c2时,x=$\frac{3+\sqrt{3}}{8}$c,
所以c<b≤$\frac{3+\sqrt{3}}{8}$c.
点评 本题考查分段函数的值域和最值的求法,注意运用分类讨论的思想方法和函数的单调性,考查运算能力,属于难题.

| A. | 28 | B. | 32 | C. | 35 | D. | 28或-21 |
| A. | 44 | B. | 66 | C. | 100 | D. | 132 |
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产缺损零件数y(件) | 11 | 9 | 8 | 5 |
(2)如果y与x线性相关,求出回归方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围?
| A. | ∅ | B. | {y|y=x2} | C. | {y|y=2x} | D. | {y|y=lgx} |
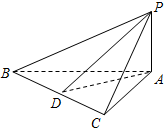 如图,在△ABC中,∠BAC=90°,PA⊥面ABC,AB=AC,D是BC的中点,则图中直角三角形的个数是8.
如图,在△ABC中,∠BAC=90°,PA⊥面ABC,AB=AC,D是BC的中点,则图中直角三角形的个数是8.