题目内容
15．若集合P={y|y=$\sqrt{x}$，x≥0}，P∩Q=Q，则集合Q不可能是（ ）| A． | ∅ | B． | {y|y=x2} | C． | {y|y=2x} | D． | {y|y=lgx} |
分析 求出p为[0，+∞），利用P∩Q=Q，得出Q⊆P，再根据函数的性质求出值域即可判断．
解答 解：∵集合P={y|y=$\sqrt{x}$，x≥0}，
∴y≥0，P为[0，+∞），
∵P∩Q=Q，∴得出Q⊆P，
∵y=lgx的值域为（-∞，+∞），
∴D不可能，
故选：D
点评 本题考察了常见的函数的值域，集合的关系，属于中档题，知识综合多点，但是难度不大．
练习册系列答案
相关题目
3．函数f（x）=$\frac{\sqrt{2x+1}}{x-3}$的定义域为（ ）
| A． | {x|x≥-$\frac{1}{2}$} | B． | {x|x＞-$\frac{1}{2}$且x≠3} | C． | {x|x≥-$\frac{1}{2}$且x≠3} | D． | {x|x≠3} |
10．设a＞0，b＞0．若$\sqrt{3}$是3a与3b的等比中项，则$\frac{1}{a}$+$\frac{1}{b}$的最小值为（ ）
| A． | 4 | B． | 6 | C． | 2$\sqrt{3}$ | D． | 2$\root{4}{3}$ |
4．
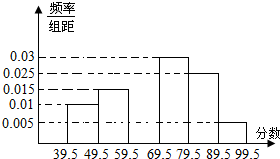如图，从参加环保知识竞赛的学生中抽出60名，将其成绩（均为整数）整理后画出的频率分布表和频率分布直方图如下，回答下列问题：
（1）分别求出a，b，x，y的值，并补全频率分布直方图；
（2）估计这次环保知识竞赛平均分；
（3）若从所有参加环保知识竞赛的学生中随机抽取一人采访，抽到的学生成绩及格的概率有多大？
如图，从参加环保知识竞赛的学生中抽出60名，将其成绩（均为整数）整理后画出的频率分布表和频率分布直方图如下，回答下列问题：| 分组 | 人数 | 频率 |
| [39.5，49.5） | a | 0.10 |
| [49.5，59.5） | 9 | x |
| [59.5，69.5） | b | 0.15 |
| [69.5，79.5） | 18 | 0.30 |
| [79.5，89.5） | 15 | y |
| [89.5，99.5] | 3 | 0.05 |
（2）估计这次环保知识竞赛平均分；
（3）若从所有参加环保知识竞赛的学生中随机抽取一人采访，抽到的学生成绩及格的概率有多大？
5．函数$y=cos（x+\frac{π}{12}）$的图象的一条对称轴的方程是（ ）
| A． | $x=\frac{5π}{12}$ | B． | x=$\frac{π}{6}$ | C． | x=$\frac{π}{12}$ | D． | x=-$\frac{π}{12}$ |