在Rt△ABC中.∠A=30°.动点D在斜边AB上运动.则∠BCD≤60°的概率为$\frac{1}{2}$．题目和参考答案——青夏教育精英家教网—

题目内容

14．在Rt△ABC中，∠A=30°，动点D在斜边AB上运动，则∠BCD≤60°的概率为$\frac{1}{2}$．

分析由题意，本题符合几何概型，设AB中点为E，当D在AE上时，∠BCD≤60°，由此得到所求．

解答解：设AB中点为E，当D在AE上时，∠BCD≤60°，由几何概型公式得到∠BCD≤60°的概率为$\frac{AE}{AB}=\frac{1}{2}$；
故答案为：$\frac{1}{2}$

点评本题考查了几何概型的概率求法；关键是明确符合条件的测度，利用公式解答．

练习册系列答案

5．已知函数f（x）=x²+3x|x-c|，其中c∈R．
（1）当$c=\frac{1}{3}$时，是否存在区间[a，b]，使得函数f（x）的定义域与值域均为[a，b]？若存在，求出所有可能的区间[a，b]，若不存在请说明理由．
（2）若c＞0，函数f（x）在区间（a，b）上既有最大值又有最小值，请分别求出a，b的取值范围（用c表示）．

2．已知正项数列{a_n}的前n项和为S_n，a₁=2，4S_n=a_n•a_n+1
（1）求{a_n}的通项公式．
（2）设数列{${\frac{1}{a_n^2}$}的前n项和为T_n，求证：$\frac{n}{4n+4}$＜T_n＜$\frac{1}{2}$．

9．现有3名老师，8名男生和5名女生共16人，若需1名老师和1名学生参加，则不同的选法种数为（　　）

19．设O为△ABC的外心（三角形外接圆的心），若$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\frac{1}{2}$|$\overrightarrow{AB}$|²，则$\frac{AC}{AB}$=（　　）

6．已知$\overrightarrow{a}=（λ，2）\overrightarrow{b}=（-3，5）$，且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为直角，则λ的值是$\frac{10}{3}$．

3．函数f（x）=$\frac{\sqrt{2x+1}}{x-3}$的定义域为（　　）

A．

{x|x≥-$\frac{1}{2}$}

B．

{x|x＞-$\frac{1}{2}$且x≠3}

C．

{x|x≥-$\frac{1}{2}$且x≠3}

D．

{x|x≠3}

4．

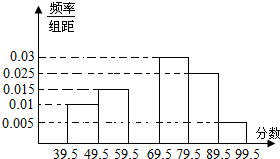如图，从参加环保知识竞赛的学生中抽出60名，将其成绩（均为整数）整理后画出的频率分布表和频率分布直方图如下，回答下列问题：

分组	人数	频率
[39.5，49.5）	a	0.10
[49.5，59.5）	9	x
[59.5，69.5）	b	0.15
[69.5，79.5）	18	0.30
[79.5，89.5）	15	y
[89.5，99.5]	3	0.05

（1）分别求出a，b，x，y的值，并补全频率分布直方图；
（2）估计这次环保知识竞赛平均分；
（3）若从所有参加环保知识竞赛的学生中随机抽取一人采访，抽到的学生成绩及格的概率有多大？

试题分类