题目内容
17.一台机器由于使用时间较长,生产的零件有一些会缺损,按不同转速生产出来的零件有缺损的统计数据如下表:| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产缺损零件数y(件) | 11 | 9 | 8 | 5 |
(2)如果y与x线性相关,求出回归方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围?
分析 (1)利用所给的数据画出散点图;
(2)先做出横标和纵标的平均数,做出利用最小二乘法求线性回归方程的系数的量,做出回归系数,写出线性回归方程.
(3)根据上一问做出的线性回归方程,使得函数值小于或等于10,解不等式可得答案.
解答 解:(1)根据表中的数据画出散点图如图: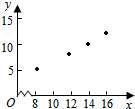
(2)设回归直线方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并列表如下:
| i | 1 | 2 | 3 | 4 |
| xi | 16 | 14 | 12 | 8 |
| yi | 11 | 9 | 8 | 5 |
| xiyi | 176 | 126 | 96 | 40 |
∴$\widehat{b}$=$\frac{438-4×12.5×8.25}{660-4×12.52}$≈0.73,$\widehat{a}$=8.25-0.73×12.5=-0.875,
∴$\widehat{y}$=0.73x-0.875.
(3)令0.73x-0.875≤10,解得x≤14.9≈15.
故机器的运转速度应控制在15转/秒内.
点评 本题考查线性回归方程的求法,考查最小二乘法,是一个基础题,解题时运算量比较大,注意利用公式求系数时,不要在运算上出错.属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
7.函数$y=cos(\frac{π}{3}-\frac{2}{5}x)$的最小正周期是( )
| A. | $\frac{π}{5}$ | B. | $\frac{5}{2}π$ | C. | -5π | D. | 5π |
12.已知双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的上、下焦点分别为F1、F2,点P为双曲线上一点,且sin∠PF1F2=$\frac{3}{5}$,若线段PF1的垂直平分线恰好经过F2,则双曲线的离心率是( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{16}{5}$ | D. | $\frac{6}{5}$ |
9.现有3名老师,8名男生和5名女生共16人,若需1名老师和1名学生参加,则不同的选法种数为( )
| A. | 39种 | B. | 24种 | C. | 15种 | D. | 16种 |