Question

9．已知点P（1，2）及圆C：x²+y²+4x-12y+24=0．若直线l过点P且被圆C截得的线段长为2$\sqrt{7}$，求l的方程．

Answer 1

分析 将圆的方程化为标准方程，找出圆心C坐标与半径r，根据题意画出相应的图形，取AB的中点为D，连接CD，可得出CD垂直于AB，得出|AD|与|AC|的长，利用勾股定理求出|CD|的长，然后分两种情况考虑：（i）直线l斜率存在时，设斜率为k，表示出l方程，由C到l的距离为3，利用点到直线的距离公式求出k的值，确定出此时l的方程；（ii）当直线l的斜率不存在时，直线x=0满足题意，综上，得到所求的直线方程．

解答 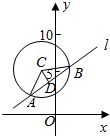解：圆的方程可化为：（x+2）²+（y-6）²=16，
∴圆心C坐标为（-2，6），半径r=4，
如图所示，|AB|=2$\sqrt{7}$，设D是线段AB的中点，则CD⊥AB，
∴|AD|=$\sqrt{7}$，
又∵|AC|=4．
故在Rt△ACD中，可得|CD|=3…（5分）
∴当直线l的斜率不存在时，满足题意，此时方程为x=1．
当直线l的斜率存在时，设所求直线l的斜率为k，则直线l的方程为：y-2=k（x-1），
由点C到直线AB的距离公式：$\frac{|-2k-6-k+2|}{\sqrt{{k}^{2}+1}}$=3，得k=-$\frac{7}{24}$．
此时，直线l的方程为7x+24y-41=0…（11分）
∴所求直线l的方程为x=1或37x+24y-41=0…（12分）

点评 此题考查了直线与圆的位置关系，涉及的知识有：垂径定理，勾股定理，点到直线的距离公式，利用了数形结合及分类讨论的思想，是一道综合性较强的试题．