题目内容
等差数列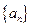 的前n项和为
的前n项和为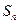 ,已知
,已知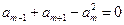 ,
,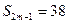 ,则
,则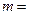
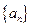 的前n项和为
的前n项和为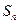 ,已知
,已知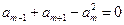 ,
,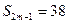 ,则
,则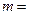
| A.38 | B.20 | C.10 | D.9 |
C
因为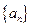 是等差数列,所以
是等差数列,所以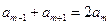 ,由
,由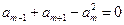 ,得:2
,得:2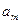 -
-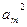 =0,所以,
=0,所以,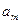 =2,又
=2,又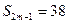 ,即
,即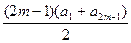 =38,即(2m-1)×2=38,解得m=10,故选C。
=38,即(2m-1)×2=38,解得m=10,故选C。
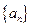 是等差数列,所以
是等差数列,所以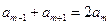 ,由
,由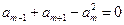 ,得:2
,得:2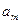 -
-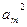 =0,所以,
=0,所以,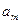 =2,又
=2,又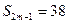 ,即
,即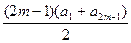 =38,即(2m-1)×2=38,解得m=10,故选C。
=38,即(2m-1)×2=38,解得m=10,故选C。
练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
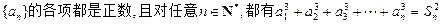 ,
,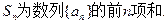
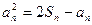 ;
;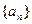 的通项公式;
的通项公式;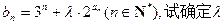 的取值范围,使得对任意
的取值范围,使得对任意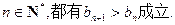
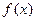 ,存在实数
,存在实数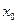 ,使得对于任意实数
,使得对于任意实数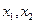 ,总有
,总有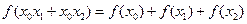 恒成立。
恒成立。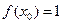 ,且对任意正整数
,且对任意正整数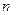 ,有
,有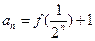 , ,求数列{an}的通项公式;
, ,求数列{an}的通项公式;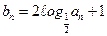 ,将数列{bn}的项重新组合成新数列
,将数列{bn}的项重新组合成新数列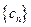 ,具体法则如下:
,具体法则如下: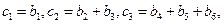
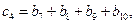 ……,求证:
……,求证: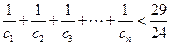 。
。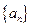 的前
的前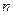 项和为
项和为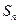 ,且对任意的
,且对任意的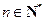 ,都有
,都有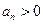 ,
,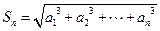 .
.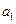 ,
,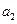 的值;
的值;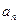 ;
;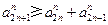 .
. 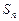 是数列
是数列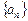 的前n项和,
的前n项和,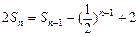 ,
,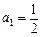
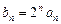 ,证明:数列
,证明:数列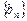 是等差数列;
是等差数列;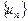 ,若存在常数M>0,对任意的
,若存在常数M>0,对任意的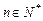 ,恒有
,恒有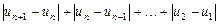 ≤M成立,称数列
≤M成立,称数列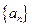 的前
的前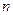 项和为
项和为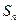 ,对任意的正整数
,对任意的正整数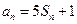 成立,记
成立,记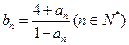 。
。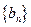 的通项公式;
的通项公式;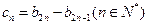 ,设数列
,设数列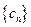 的前
的前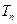 ,求证:对任意正整数
,求证:对任意正整数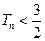 ;
;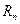 。已知正实数
。已知正实数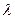 满足:对任意正整数
满足:对任意正整数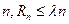 恒成立,求
恒成立,求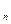 }中,a
}中,a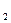 =2,前n项和为S
=2,前n项和为S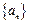 的前
的前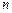 项和
项和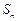 满足
满足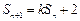 ,且
,且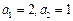

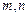 ,使
,使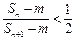 成立?若存在,求出这样的正整数;若不存在,说明理由.
成立?若存在,求出这样的正整数;若不存在,说明理由.