题目内容
已知数列{a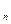 }中,a
}中,a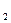 =2,前n项和为S
=2,前n项和为S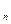 ,且S
,且S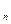 =.
=.
(1)证明数列{an+1-an}是等差数列,并求出数列{an}的通项公式
(2)设bn=,数列{bn}的前n项和为Tn,求使不等式Tn>
对一切n∈N*都成立的最大正整数k的值
 }中,a
}中,a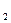 =2,前n项和为S
=2,前n项和为S ,且S
,且S =.
=.(1)证明数列{an+1-an}是等差数列,并求出数列{an}的通项公式
(2)设bn=,数列{bn}的前n项和为Tn,求使不等式Tn>
对一切n∈N*都成立的最大正整数k的值
(Ⅰ)an=n(n∈N*) ;(Ⅱ)k的最大值为18;
(1)由题意,当n=1时,a1=S1=,则a1=1,a2=2,则a2-a1=1,
当n≥2时,an=Sn-Sn-1=-=[nan-(n-1)an-1+1]an+1=[(n+1)an+1-nan+1]
则an+1-an=[(n+1)an+1-2nan+(n-1)an-1],
即(n-1)an+1-2(n-1)an+(n-1)an-1=0,
即an+1-2an+an-1="0, " 即an+1-an=an-an-1
则数列{an+1-an}是首项为1,公差为0的等差数列.
从而an-an-1=1,,则数列{an}是首项为1,公差为1的等差数列,
所以,an=n(n∈N*)
(2)bn===(- )
所以,Tn=b1+b2+…+bn=[(1-)+(-)+…+(-)]
=(1-)=
由于Tn+1-Tn=-=>0,
因此Tn单调递增,故Tn的最小值为T1=
令>,得k<19,所k的最大值为18
当n≥2时,an=Sn-Sn-1=-=[nan-(n-1)an-1+1]an+1=[(n+1)an+1-nan+1]
则an+1-an=[(n+1)an+1-2nan+(n-1)an-1],
即(n-1)an+1-2(n-1)an+(n-1)an-1=0,
即an+1-2an+an-1="0, " 即an+1-an=an-an-1
则数列{an+1-an}是首项为1,公差为0的等差数列.
从而an-an-1=1,,则数列{an}是首项为1,公差为1的等差数列,
所以,an=n(n∈N*)
(2)bn===(- )
所以,Tn=b1+b2+…+bn=[(1-)+(-)+…+(-)]
=(1-)=
由于Tn+1-Tn=-=>0,
因此Tn单调递增,故Tn的最小值为T1=
令>,得k<19,所k的最大值为18

练习册系列答案
相关题目
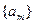 是首项为,公差为
是首项为,公差为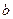 的等差数列,
的等差数列,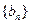 是首项为
是首项为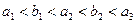 ,其中
,其中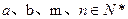 .
.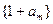 与数列
与数列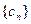 ,求数列
,求数列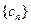 的通项公式;
的通项公式;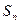 ,求证:
,求证: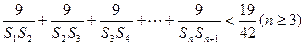 .
.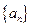 的前三项之积为512,且这三项分别减去1,3,9后又成等差数列,求数列
的前三项之积为512,且这三项分别减去1,3,9后又成等差数列,求数列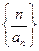 的前n项和
的前n项和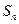 .
.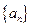 的前n项和为
的前n项和为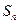 ,已知
,已知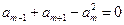 ,
,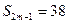 ,则
,则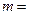
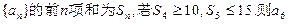 的最大值为 。
的最大值为 。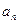 }中,
}中,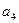 =14,前10项和
=14,前10项和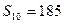 .
.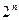 项按原来的顺序排成一个新数列,求此数列的前
项按原来的顺序排成一个新数列,求此数列的前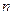 项和
项和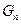 .
.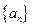 和
和 的前n项和分别为
的前n项和分别为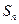 和
和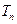 ,若对一切正整数n都有
,若对一切正整数n都有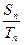 =
=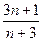 ,则
,则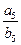 的值为 .
的值为 .