题目内容
已知定义在R上的单调函数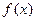 ,存在实数
,存在实数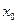 ,使得对于任意实数
,使得对于任意实数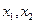 ,总有
,总有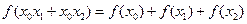 恒成立。
恒成立。
(Ⅰ)求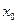 的值;
的值;
(Ⅱ)若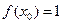 ,且对任意正整数
,且对任意正整数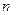 ,有
,有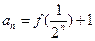 , ,求数列{an}的通项公式;
, ,求数列{an}的通项公式;
(Ⅲ)若数列{bn}满足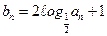 ,将数列{bn}的项重新组合成新数列
,将数列{bn}的项重新组合成新数列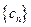 ,具体法则如下:
,具体法则如下: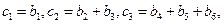
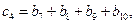 ……,求证:
……,求证: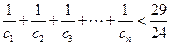 。
。
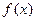 ,存在实数
,存在实数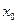 ,使得对于任意实数
,使得对于任意实数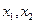 ,总有
,总有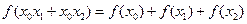 恒成立。
恒成立。(Ⅰ)求
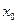 的值;
的值;(Ⅱ)若
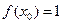 ,且对任意正整数
,且对任意正整数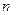 ,有
,有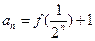 , ,求数列{an}的通项公式;
, ,求数列{an}的通项公式;(Ⅲ)若数列{bn}满足
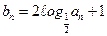 ,将数列{bn}的项重新组合成新数列
,将数列{bn}的项重新组合成新数列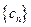 ,具体法则如下:
,具体法则如下: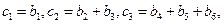
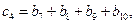 ……,求证:
……,求证: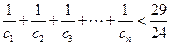 。
。(Ⅰ)
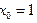 (Ⅱ)
(Ⅱ)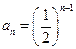 (Ⅲ)见解析
(Ⅲ)见解析(Ⅰ)令
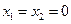 ,得
,得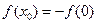 ,①
,①令
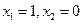 ,得
,得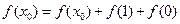 ,
,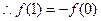 ,②
,②由①、②得
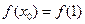 ,又因为
,又因为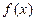 为单调函数,
为单调函数,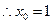 ……(2分)
……(2分)(Ⅱ)由(1)得
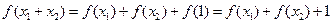 ,
,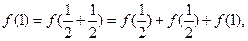
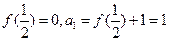
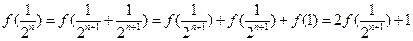 ,……(3分)
,……(3分) ……(4分)
……(4分)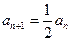 ,
,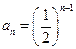 ,……(5分)
,……(5分)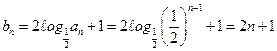 ……(6分)
……(6分)(Ⅲ)由{Cn}的构成法则可知,Cn应等于{bn}中的n项之和,其第一项的项数为
[1+2+…+(n-1)]+1=
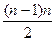 +1,即这一项为2×[
+1,即这一项为2×[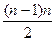 +1]-1=n(n-1)+1
+1]-1=n(n-1)+1Cn=n(n-1)+1+n(n-1)+3+…+n(n-1)+2n-1=n2(n-1)+
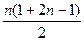 =n3……(8分)
=n3……(8分)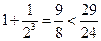
当
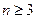 时,
时,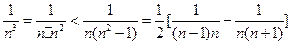 ……(12分)
……(12分)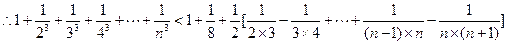
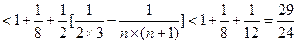 ……(14分)
……(14分)解法2:
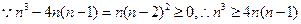
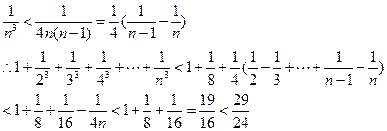

练习册系列答案
相关题目
 中,
中,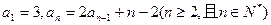
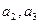 的值;
的值;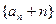 是等比数列,并求
是等比数列,并求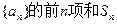 。
。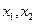 (
(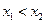 )是方程
)是方程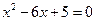 的两根,且
的两根,且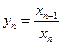 ,
,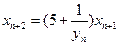 .
. 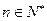 (1)求
(1)求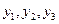 的值;(2)设
的值;(2)设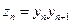 ,求证:
,求证: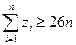 ;(3)求证:对
;(3)求证:对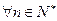 有
有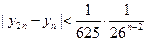 w。.w..
w。.w.. 的前
的前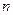 项和为
项和为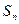 ,且满足
,且满足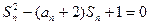 ,
,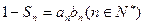 .
.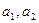 的值;
的值;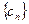 满足
满足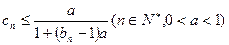 ,
,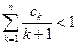 .
.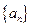 的前三项之积为512,且这三项分别减去1,3,9后又成等差数列,求数列
的前三项之积为512,且这三项分别减去1,3,9后又成等差数列,求数列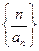 的前n项和
的前n项和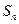 .
.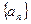 中,
中,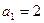 ,
,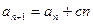 (
(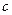 是常数,
是常数,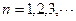 ),且
),且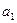 ,
,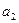 ,
,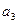 成公比不为
成公比不为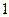 的等比数列.
的等比数列.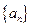 的前n项和为
的前n项和为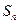 ,已知
,已知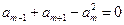 ,
,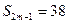 ,则
,则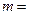
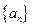 和
和 的前n项和分别为
的前n项和分别为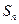 和
和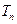 ,若对一切正整数n都有
,若对一切正整数n都有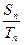 =
=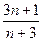 ,则
,则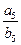 的值为 .
的值为 .