题目内容
设数列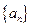 的前
的前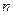 项和为
项和为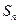 ,且对任意的
,且对任意的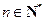 ,都有
,都有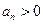 ,
,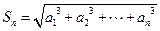 .
.
(1)求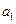 ,
,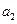 的值;
的值;
(2)求数列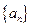 的通项公式
的通项公式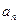 ;
;
(3)证明: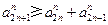 .
.
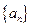 的前
的前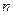 项和为
项和为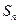 ,且对任意的
,且对任意的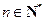 ,都有
,都有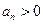 ,
,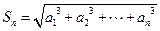 .
.(1)求
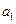 ,
,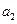 的值;
的值;(2)求数列
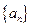 的通项公式
的通项公式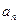 ;
;(3)证明:
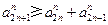 .
. (1)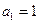
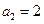 (2)
(2)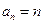 (3)见解析
(3)见解析
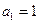
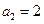 (2)
(2)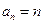 (3)见解析
(3)见解析 (1)解:当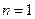 时,有
时,有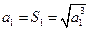 ,
,
由于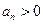 ,所以
,所以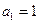 .
.
当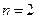 时,有
时,有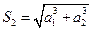 ,即
,即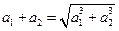 ,
,
将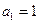 代入上式,由于
代入上式,由于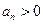 ,所以
,所以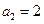 .
.
(2)解:由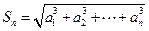 ,
,
得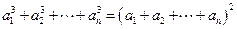 , ①
, ①
则有 . ②
. ②
②-①,得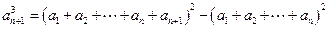 ,
,
由于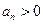 ,所以
,所以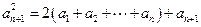 . ③
. ③
同样有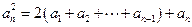
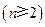 , ④
, ④
③-④,得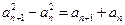 .
.
所以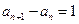 .
.
由于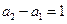 ,即当
,即当 时都有
时都有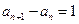 ,所以数列
,所以数列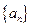 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.
故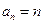 .
.
(3)证明1:由于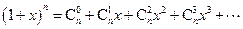 ,
,
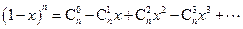 ,
,
所以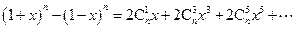 .
.
即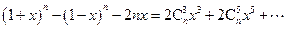 .
.
令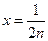 ,则有
,则有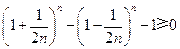 .
.
即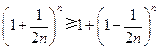 ,
,
即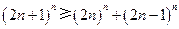
故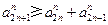 .
.
证明2:要证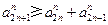 ,
,
只需证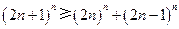 ,
,
只需证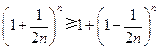 ,
,
只需证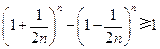 .
.
由于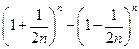
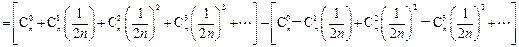
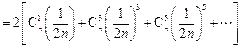
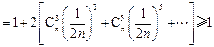 .
.
因此原不等式成立.
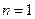 时,有
时,有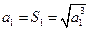 ,
,由于
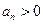 ,所以
,所以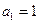 .
. 当
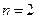 时,有
时,有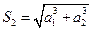 ,即
,即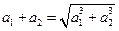 ,
,将
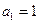 代入上式,由于
代入上式,由于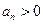 ,所以
,所以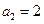 .
. (2)解:由
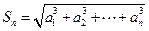 ,
,得
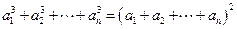 , ①
, ①则有
 . ②
. ②②-①,得
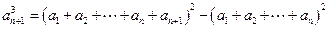 ,
, 由于
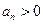 ,所以
,所以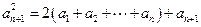 . ③
. ③同样有
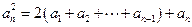
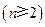 , ④
, ④③-④,得
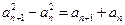 .
.所以
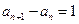 .
.由于
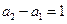 ,即当
,即当 时都有
时都有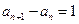 ,所以数列
,所以数列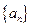 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.故
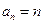 .
. (3)证明1:由于
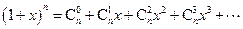 ,
,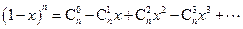 ,
, 所以
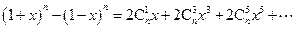 .
. 即
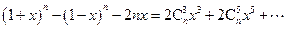 .
.令
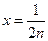 ,则有
,则有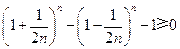 .
.即
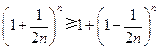 ,
,即
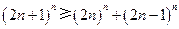
故
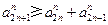 .
. 证明2:要证
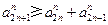 ,
,只需证
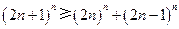 ,
,只需证
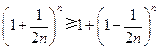 ,
,只需证
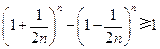 .
. 由于
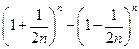
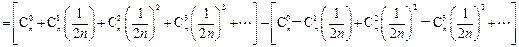
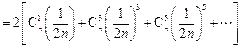
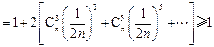 .
.因此原不等式成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
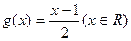 ,且数列
,且数列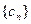 满足
满足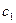 = 1,
= 1,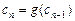 (n∈N,
(n∈N,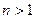 );求数列
);求数列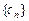 的通项公式.
的通项公式.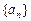 、
、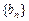 的前n项和分别为
的前n项和分别为 和
和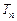 ,且
,且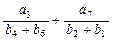
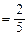 ,
,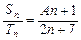 ,
, 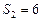 ;求常数A的值及
;求常数A的值及 ,其中
,其中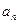 、
、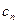 即为(1)、(2)中的数列
即为(1)、(2)中的数列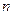 项,试求
项,试求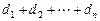
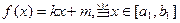 时,
时,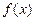 的值域为
的值域为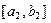 ,当
,当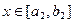
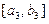 ,依次类推,一般地,当
,依次类推,一般地,当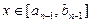 时,
时,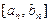 ,其中k、m为常数,且
,其中k、m为常数,且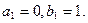
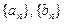 的通项公式;
的通项公式;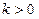 ,使得数列
,使得数列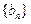 满足
满足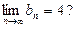 若存在,求k的值;若不存在,请说明理由;
若存在,求k的值;若不存在,请说明理由;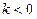 ,设数列
,设数列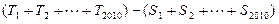 。
。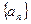 中,
中,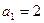 ,
,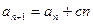 (
(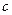 是常数,
是常数,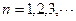 ),且
),且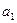 ,
,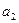 ,
,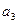 成公比不为
成公比不为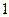 的等比数列.
的等比数列.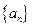 的前
的前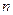 项和为
项和为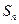 。已知
。已知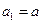 ,
,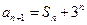 ,
,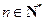 。
。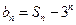 ,求数列
,求数列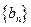 的通项公式;
的通项公式;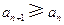 ,
,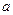 的取值范围。
的取值范围。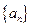 的前n项和为
的前n项和为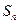 ,已知
,已知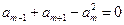 ,
,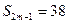 ,则
,则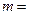
 和
和 都是等差数列,其中a1=5,b1=10,且a50+b50=20,则数列
都是等差数列,其中a1=5,b1=10,且a50+b50=20,则数列 的前50项和为( )
的前50项和为( ) 中,
中, ,数列
,数列 满足
满足 ,且
,且 (1)求数列
(1)求数列 的前
的前 项的和
项的和 .
.