题目内容
已知数列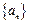 的前
的前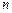 项和
项和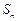 满足
满足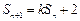 ,且
,且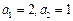

(1)求k的值;
(2)求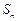 ;
;
(3)是否存在正整数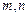 ,使
,使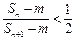 成立?若存在,求出这样的正整数;若不存在,说明理由.
成立?若存在,求出这样的正整数;若不存在,说明理由.
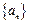 的前
的前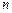 项和
项和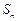 满足
满足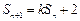 ,且
,且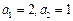

(1)求k的值;
(2)求
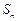 ;
;(3)是否存在正整数
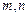 ,使
,使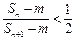 成立?若存在,求出这样的正整数;若不存在,说明理由.
成立?若存在,求出这样的正整数;若不存在,说明理由.(1)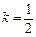 ;(2)
;(2)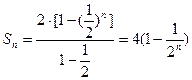 ;(3)存在正整数
;(3)存在正整数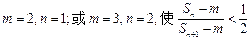
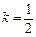 ;(2)
;(2)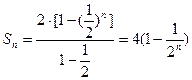 ;(3)存在正整数
;(3)存在正整数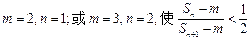
(1) 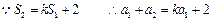
又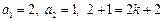 ,∴
,∴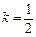

(2) 由 (1) 知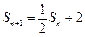 ①
①
当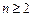 时,
时,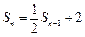 ②
②
①-②,得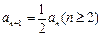
又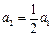 ,易见
,易见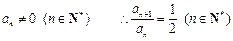
于是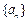 是等比数列,公比为
是等比数列,公比为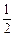 ,所以
,所以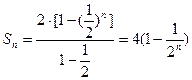
(3) 不等式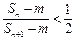 ,即
,即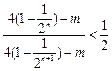 .;整理得
.;整理得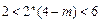
假设存在正整数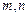 使得上面的不等式成立,由于2n为偶数,
使得上面的不等式成立,由于2n为偶数,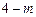 为整数,
为整数,
则只能是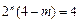
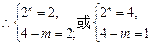
因此,存在正整数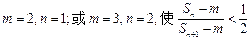
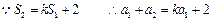
又
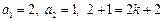 ,∴
,∴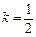

(2) 由 (1) 知
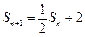 ①
①当
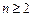 时,
时,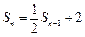 ②
②①-②,得
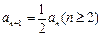
又
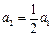 ,易见
,易见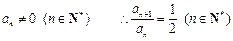
于是
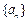 是等比数列,公比为
是等比数列,公比为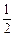 ,所以
,所以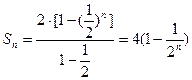
(3) 不等式
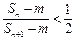 ,即
,即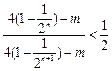 .;整理得
.;整理得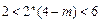
假设存在正整数
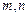 使得上面的不等式成立,由于2n为偶数,
使得上面的不等式成立,由于2n为偶数,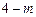 为整数,
为整数,则只能是
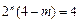
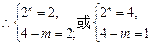
因此,存在正整数
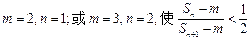

练习册系列答案
相关题目
 的前
的前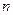 项和为
项和为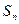 ,且满足
,且满足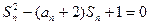 ,
,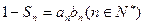 .
.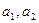 的值;
的值;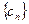 满足
满足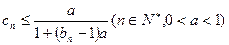 ,
,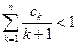 .
. 平面上有一系列点
平面上有一系列点
 对每个自然数
对每个自然数 ,点
,点 位于函数
位于函数 的图象上.以点
的图象上.以点 与
与 轴都相切,且⊙
轴都相切,且⊙ 又彼此外切.若
又彼此外切.若 ,且
,且
 .
. 是等差数列;
是等差数列; ,
, , 求证:
, 求证:
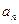 }的前n项和为
}的前n项和为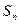 ,且
,且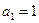 ,
,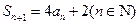 .
.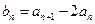 ,求证:数列{
,求证:数列{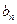 }是等比数列;
}是等比数列;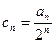 ,求证:数列{
,求证:数列{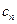 }是等差数列;
}是等差数列;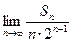 .
.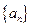 的前n项和为
的前n项和为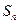 ,已知
,已知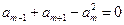 ,
,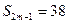 ,则
,则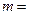
 为二次函数,不等式
为二次函数,不等式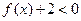 的解集为
的解集为 ,且对任意
,且对任意 ,恒有
,恒有 .
.  满足
满足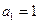 ,
,
 .
.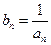 ,求数列
,求数列 的通项公式;
的通项公式; 项和为
项和为 ,求数列
,求数列 的前
的前 .
.  中,
中, ,数列
,数列 满足
满足 ,且
,且 (1)求数列
(1)求数列 的前
的前 项的和
项的和 .
.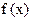 ,若存在
,若存在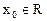 ,使
,使 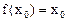 成立,则称
成立,则称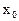 为
为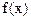 的“滞点”.已知函数f ( x ) =
的“滞点”.已知函数f ( x ) = 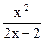 .
.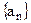 的各项均为负数,且满足
的各项均为负数,且满足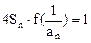 ,求数列
,求数列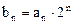 ,求
,求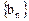 的前项和
的前项和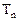 .
.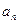 }中,
}中,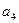 =14,前10项和
=14,前10项和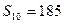 .
.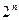 项按原来的顺序排成一个新数列,求此数列的前
项按原来的顺序排成一个新数列,求此数列的前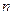 项和
项和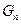 .
.