题目内容
20.过点A(-1,0)且斜率为k(k>0)的直线与抛物线y2=4x相交于B,C两点,若|AB|=$\frac{1}{3}$|BC|,则k等于( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
分析 根据题意表示出直线方程,代入抛物线方程消去x,利用求根公式求出B,C的纵坐标,利用|AB|=$\frac{1}{3}$|BC|,建立等式,把A,B的纵坐标带入即可求得k.
解答  解:依题意知直线方程为y=k(x+1),代入抛物线方程,整理得ky2-4y+4k=0,
解:依题意知直线方程为y=k(x+1),代入抛物线方程,整理得ky2-4y+4k=0,
解得yB=$\frac{2-2\sqrt{1-{k}^{2}}}{k}$,yC=$\frac{2+2\sqrt{1-{k}^{2}}}{k}$,
∵|AB|=$\frac{1}{3}$|BC|,∴yB=$\frac{1}{4}$yC,
∴$\frac{2-2\sqrt{1-{k}^{2}}}{k}$=$\frac{1}{4}$•$\frac{2+2\sqrt{1-{k}^{2}}}{k}$,
∵k>0,∴求得k=$\frac{4}{5}$.
故选:C.
点评 本题主要考查了直线与抛物线的位置关系.一般解法是设出直线方程,与抛物线方程联立进行消元,利用转化为一元二次方程的问题进行解决.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.设a,b∈R,则“a=0”是“ab=0”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.已知sin($\frac{π}{2}$+θ)=$\frac{1}{3}$,则2sin2$\frac{θ}{2}$-1等于( )
| A. | $\frac{\sqrt{2}}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | ±$\frac{2\sqrt{2}}{3}$ |
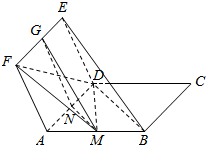 如图,ABCD与ADEF均为平行四边形,M,N,G分别是AB,AD,EF的中点.
如图,ABCD与ADEF均为平行四边形,M,N,G分别是AB,AD,EF的中点.