题目内容
10.已知方程$\frac{{x}^{2}}{2-k}$+$\frac{{y}^{2}}{k-1}$=1表示双曲线,求k的取值范围,并写出焦点坐标.分析 由题意,(2-k)(k-1)<0,即可求k的取值范围;分类讨论,即可求双曲线C的焦点坐标.
解答 解:由题意,(2-k)(k-1)<0,
∴k<1或k>2;
k<1,双曲线的焦点在x轴上,a2=2-k,b2=1-k,c2=3-2k,∴双曲线C的焦点坐标为(±$\sqrt{3-2k}$,0).
k>2,双曲线的焦点在y轴上,a2=k-1,b2=k-2,c2=2k-3,∴双曲线C的焦点坐标为(0,±$\sqrt{2k-3}$).
点评 本题考查双曲线的方程与性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
20.过点A(-1,0)且斜率为k(k>0)的直线与抛物线y2=4x相交于B,C两点,若|AB|=$\frac{1}{3}$|BC|,则k等于( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
1.将-$\frac{25}{6}$π化成a+2kπ(k∈Z,0≤a<2π)的形式为( )
| A. | -$\frac{25}{6}$π=-5π+$\frac{5}{6}$π | B. | -$\frac{25}{6}$π=-6π+$\frac{11}{6}$π | C. | -$\frac{25}{6}$π=-4π-$\frac{π}{6}$ | D. | -$\frac{25}{6}$π=-3π-$\frac{7}{6}$π |
15.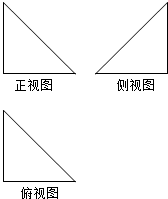 若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形,则这个空间几何体的外接球的表面积和内切球的表面积之比是( )
若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形,则这个空间几何体的外接球的表面积和内切球的表面积之比是( )
 若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形,则这个空间几何体的外接球的表面积和内切球的表面积之比是( )
若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形,则这个空间几何体的外接球的表面积和内切球的表面积之比是( )| A. | $\frac{18+9\sqrt{3}}{2}$ | B. | 18+9$\sqrt{3}$ | C. | 3 | D. | 9 |
1.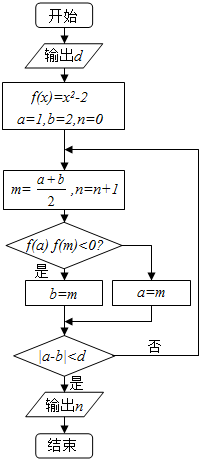 执行如图的程序框图,如果输入的d=0.01,则输出的n=( )
执行如图的程序框图,如果输入的d=0.01,则输出的n=( )
 执行如图的程序框图,如果输入的d=0.01,则输出的n=( )
执行如图的程序框图,如果输入的d=0.01,则输出的n=( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |