题目内容
5．已知sin（$\frac{π}{2}$+θ）=$\frac{1}{3}$，则2sin2$\frac{θ}{2}$-1等于（ ）| A． | $\frac{\sqrt{2}}{3}$ | B． | -$\frac{1}{3}$ | C． | $\frac{1}{3}$ | D． | ±$\frac{2\sqrt{2}}{3}$ |
分析 利用诱导公式及二倍角公式即可计算求值．
解答 解：∵sin（$\frac{π}{2}$+θ）=cosθ=$\frac{1}{3}$，
∴2sin2$\frac{θ}{2}$-1=-（1-2sin2$\frac{θ}{2}$）=-cosθ=-$\frac{1}{3}$．
故选：B．
点评 本题主要考查了诱导公式及二倍角公式的应用，属于基础题．
练习册系列答案
应用题作业本系列答案
相关题目
15．已知a=0.2-0.2，b=log0.52，c=$\frac{\root{3}{2}}{2}$，则a，b，c的大小关系正确的是（ ）
| A． | a＜b＜c | B． | b＜c＜a | C． | c＜b＜a | D． | c＜a＜b |
16．下列各函数中，图象完全相同的是（ ）
| A． | y=2lgx和y=lgx2 | B． | y=$\frac{|x-1|}{x-1}$和y=$\left\{\begin{array}{l}{-1，x∈（-∞，1）}\\{1，x∈（1，+∞）}\end{array}\right.$ | ||
| C． | y=$\frac{{x}^{2}}{x}$和y=x | D． | y=x-3和y=$\sqrt{（x-3）^{2}}$ |
20．过点A（-1，0）且斜率为k（k＞0）的直线与抛物线y2=4x相交于B，C两点，若|AB|=$\frac{1}{3}$|BC|，则k等于（ ）
| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{4}{5}$ | D． | $\frac{3}{4}$ |
15．
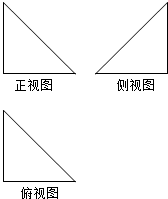若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形，则这个空间几何体的外接球的表面积和内切球的表面积之比是（ ）
若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形，则这个空间几何体的外接球的表面积和内切球的表面积之比是（ ）| A． | $\frac{18+9\sqrt{3}}{2}$ | B． | 18+9$\sqrt{3}$ | C． | 3 | D． | 9 |