题目内容
3.定义在区间(a,a+2)上的奇函数y=f(x),当0<x<a+2时,f(x)=-($\frac{1}{2}$)x+$\frac{1}{2}$,则y的取值范围是(-$\frac{1}{2}$,0).分析 根据奇函数的性质先求出a,然后求函数的值域就可以了.
解答 解:因为定义在区间(a,a+2)上的奇函数y=f(x),
所以a+a+2=0,
解得:a=-1,
∴当0<x<1时,f(x)=-($\frac{1}{2}$)x+$\frac{1}{2}$∈(-$\frac{1}{2}$,0),
故答案为:(-$\frac{1}{2}$,0).
点评 本题主要考查奇函数的性质,以及函数的单调性,属于基础题.

练习册系列答案
相关题目
8.设a=log3π,b=log2$\sqrt{3}$,c=log3$\sqrt{2}$,则a、b、c的大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | b>a>c |
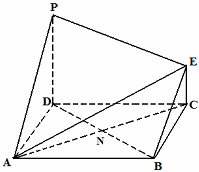 如图,已知几何体的底面ABCD 为正方形,AC∩BD=N,PD⊥平面ABCD,
如图,已知几何体的底面ABCD 为正方形,AC∩BD=N,PD⊥平面ABCD,