题目内容
13.给定正奇数n(n≥5),数列{an}:a1,a2,…an是1,2,…,n的一个排列,定义E(a1,a2,…an=|a1-1|+|a2-2|+…+|an-n|为数列{an}:a1,a2,…an的位差和.若位差和E(a1,a2,…an)=4,则满足条件的数列{an}:a1,a2,…an的个数为$\frac{(n-2)(n+3)}{2}$; (用n表示)分析 若数列{an}:a1,a2,…,an的位差和E(a1,a2,…,an)=4,有如下两种情况:
情况一:当ai=i+1,ai+1=i,aj=j+1,aj+1=j,且{ai,ai+1}∩{aj,aj+1}=∅,其他项ak=k(其中k∉{i,i+1,j,j+1})时;情况二:当ai,ai+1,ai+2分别等于i+2,i+1,i;或i+1,i+2,i;或i+2,i+1,i;其他项ak=k(其中k∉{i,i+1,i+2})时,分别计算出即可得出.
解答 解:若数列{an}:a1,a2,…,an的位差和E(a1,a2,…,an)=4,有如下两种情况:
情况一:当ai=i+1,ai+1=i,aj=j+1,aj+1=j,且{ai,ai+1}∩{aj,aj+1}=∅,其他项ak=k(其中k∉{i,i+1,j,j+1})时,有(n-3)+(n-4)+…+2+1=$\frac{(n-2)(n-3)}{2}$种可能;
情况二:当ai,ai+1,ai+2分别等于i+2,i+1,i;或i+1,i+2,i;或i+2,i+1,i;其他项ak=k(其中k∉{i,i+1,i+2})时,有3(n-2)种可能;
综上,满足条件的数列{an}:a1,a2,…,an的个数为$\frac{(n-2)(n-3)}{2}$+3(n-2)=$\frac{(n-2)(n+3)}{2}$.
故答案为:$\frac{(n-2)(n+3)}{2}$.
点评 本题考查了新定义“位差和”、等差数列的前n项和公式、分类讨论思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.定义在区间(a,a+2)上的奇函数y=f(x),当0<x<a+2时,f(x)=-($\frac{1}{2}$)x+$\frac{1}{2}$,则y的取值范围是(-$\frac{1}{2}$,0).
1.函数h(x)=2sin(2x+$\frac{π}{6}$),函数f(x)=2cos(2x-$\frac{2π}{3}$)可由h(x)经过( )的变换得到.
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
5.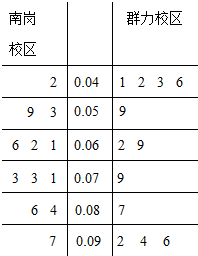 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )
 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )| A. | 南岗校区 | B. | 群力校区 | ||
| C. | 南岗、群力两个校区相等 | D. | 无法确定 |
2.已知复数z=$\frac{1-2i}{3+4i}$(i是虚数单位),则z的共轭复数的虚部是( )
| A. | -$\frac{2}{5}$i | B. | $\frac{2}{5}$i | C. | -$\frac{2}{5}$ | D. | $\frac{2}{5}$ |