题目内容
11.已知函数f(x)=(1+a)lnx,g(x)=ax-$\frac{1}{x}$(a>0).(1)若与f(x)的图象切于点A(1,f(1))的直线与函数g(x)的图象相切,求实数a的值;
(2)设F(x)=g(x)-f(x),若对任意a∈(1,3),x1,x2∈[1,3],恒有(m-ln3)a-ln3>|F(x1)-F(x2)|成立,求实数m的取值范围.
分析 (1)若与f(x)的图象切于点A(1,f(1))的直线与函数g(x)的图象相切,求出相应的切线方程,比较即可求实数a的值;
(2)求导数,确定F(x)在[1,3]上是增函数,由(m-ln3)a-ln3>|F(x1)-F(x2)|对任意的a∈(1,3),x1,x2∈[1,3]恒成立,转化为(m-ln3)a-ln3>|F(x1)-F(x2)|max,分离出参数m后再化为函数的最值即可.
解答 解:(1)∵f(x)=(1+a)lnx,
∴f′(x)=$\frac{1+a}{x}$,
∴f′(1)=1+a,
∵f(1)=0,
∴f(x)的图象在点A(1,f(1))的切线的方程为y=(1+a)(x-1)①.
由g(x)=ax-$\frac{1}{x}$,可得g′(x)=a+$\frac{1}{{x}^{2}}$,
设切点为(n,an-$\frac{1}{n}$),则切线方程为y-(an-$\frac{1}{n}$)=(a+$\frac{1}{{n}^{2}}$)(x-n),即y=(a+$\frac{1}{{n}^{2}}$)x+$\frac{2}{n}$②
①②比较可得a=-3或1;
(2)F(x)=g(x)-f(x)=ax-$\frac{1}{x}$-(1+a)lnx,
∴F′(x)=a+$\frac{1}{{x}^{2}}$-$\frac{1+a}{x}$=$\frac{a(x-1)(x-\frac{1}{a})}{{x}^{2}}$
∴a∈(1,3),
∴F(x)在[1,3]上是增函数,
∴|F(x1)-F(x2)|≤F(3)-F(1)=2a-(1+a)ln3+$\frac{2}{3}$,
由(m-ln3)a-ln3>|F(x1)-F(x2)|对任意的a∈(1,3),x1,x2∈[1,3]恒成立,
∴(m-ln3)a-ln3>|F(x1)-F(x2)|max,即(m-ln3)a-ln3>2a-(1+a)ln3+$\frac{2}{3}$任意1<a<3恒成立,
∴m>2+$\frac{2}{3a}$对任意1<a<3恒成立,
由于1<a<3,∴m>$\frac{8}{3}$.
点评 该题考查利用导数研究切线方程、最值、单调性,考查函数恒成立问题,考查转化思想,考查学生分析解决问题的能力.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
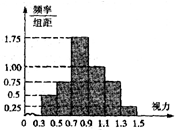 某班50名学生的高校招生体检表中的视力情况进行统计,其结果的频率分布直方图如图所示.若A高校某专业对视力的要求在1.1以上,则该班学生中能报A高校该专业的人数为( )
某班50名学生的高校招生体检表中的视力情况进行统计,其结果的频率分布直方图如图所示.若A高校某专业对视力的要求在1.1以上,则该班学生中能报A高校该专业的人数为( )| A. | 10 | B. | 20 | C. | 8 | D. | 16 |
| A. | $\overrightarrow{a}$与$\overrightarrow{b}$方向相同 | B. | $\overrightarrow{a}$与$\overrightarrow{b}$方向相反 | C. | $\overrightarrow{a}$与$\overrightarrow{b}$垂直 | D. | 以上都不对 |
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |