题目内容
13.若k∈[-2,2],则k的值使得过A(1,1)可以做两条直线与圆x2+y2+kx-2y-$\frac{5}{4}$k=0相切的概率等于$\frac{1}{4}$.分析 把圆方程化为标准方程,根据二元二次构成圆的条件求出k的范围,根据题意得到点A在圆外,确定出k的具体范围,根据已知k的范围确定出所求概率即可.
解答 解:把圆的方程化为标准方程得:(x+$\frac{k}{2}$)2+(y-1)2=1+$\frac{5}{4}$k+$\frac{1}{4}$k2,
∴1+$\frac{5}{4}$k+$\frac{1}{4}$k2>0,
解得:k<-4或k>-1,
∵点A(1,1)在已知圆的外部,
∴把点A(1,1)代入圆方程得:1+1+k-2-$\frac{5}{4}$k>0,
解得:k<0,
∴实数k的取值范围是k<-4或-1<k<0,
则k的值使得过A(1,1)可以做两条直线与圆x2+2+kx-2y-$\frac{5}{4}$k=0相切的概率P=$\frac{0-(-1)}{2-(-2)}$=$\frac{1}{4}$,
故答案为:$\frac{1}{4}$
点评 此题考查了圆的切线方程,以及概率求法,求出k的范围是解本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
4.若复数z满足z(1+i)=1-i(i是虚数单位),则z的共轭复数$\overline{z}$的虚部是( )
| A. | -i | B. | -1 | C. | i | D. | 1 |
1.已知公差不为0的等差数列{an}满足a1,a3,a4成等比数列,Sn为数列{an}的前n项和,则$\frac{{S}_{3}-{S}_{2}}{{S}_{5}-{S}_{3}}$的值为( )
| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
 如图,在△ABC中,AC=12,∠ABC=2∠C.
如图,在△ABC中,AC=12,∠ABC=2∠C.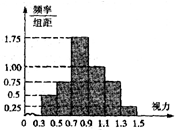 某班50名学生的高校招生体检表中的视力情况进行统计,其结果的频率分布直方图如图所示.若A高校某专业对视力的要求在1.1以上,则该班学生中能报A高校该专业的人数为( )
某班50名学生的高校招生体检表中的视力情况进行统计,其结果的频率分布直方图如图所示.若A高校某专业对视力的要求在1.1以上,则该班学生中能报A高校该专业的人数为( )