已知2cos+3cos=0.则tan2x=$\frac{12}{5}$.sin2x=$\frac{12}{13}$．题目和参考答案——青夏教育精英家教网—

题目内容

12．已知2cos（π-x）+3cos（$\frac{π}{2}$-x）=0，则tan2x=$\frac{12}{5}$，sin2x=$\frac{12}{13}$．

分析由条件利用同角三角函数的基本关系、诱导公式求得tanx的值，再利用二倍角公式求得tan2x、sin2x的值．

解答解：由于2cos（π-x）+3cos（$\frac{π}{2}$-x）=0，即-2cosx+3sinx=0，∴tanx=$\frac{2}{3}$，
∴tan2x=$\frac{2tanx}{1{-tan}^{2}x}$=$\frac{12}{5}$ sin2x=$\frac{2sinxcosx}{{sin}^{2}x{+cos}^{2}x}$=$\frac{2tanx}{{tan}^{2}x+1}$=$\frac{\frac{4}{3}}{\frac{4}{9}+1}$=$\frac{12}{13}$，
故答案为：$\frac{12}{5}$；$\frac{12}{13}$．

点评本题主要考查同角三角函数的基本关系的应用，诱导公式、二倍角公式的应用，属于基础题．

练习册系列答案

相关题目

2．

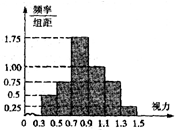某班50名学生的高校招生体检表中的视力情况进行统计，其结果的频率分布直方图如图所示．若A高校某专业对视力的要求在1.1以上，则该班学生中能报A高校该专业的人数为（　　）

3．定义在区间（a，a+2）上的奇函数y=f（x），当0＜x＜a+2时，f（x）=-（$\frac{1}{2}$）^x+$\frac{1}{2}$，则y的取值范围是（-$\frac{1}{2}$，0）．

20．已知椭圆mx²+4y²=1的离心率为$\frac{\sqrt{2}}{2}$，则实数m等于2或8．

7．

如图所示，几何体ABCDE中，△ABC为正三角形，CD⊥面ABC，BE∥CD，BC=CD=2BE．
（Ⅰ）在线段AD上找一点F，使EF∥平面ABC，并证明；
（Ⅱ）求证：面ADE⊥面ACD．

17．过椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的右焦点F作两条相互垂直的直线分别交椭圆于A，B，C，D四点，则$\frac{1}{|AB|}+\frac{1}{|CD|}$的值为（　　）

4．A、B、C、D是同一球面上的四个点，其中△ABC是正三角形，AD⊥平面ABC，AD=4，AB=2$\sqrt{3}$，则该球的表面积为32π．

1．函数h（x）=2sin（2x+$\frac{π}{6}$），函数f（x）=2cos（2x-$\frac{2π}{3}$）可由h（x）经过（　　）的变换得到．

	A．	向右平移$\frac{π}{6}$个单位		B．	向左平移$\frac{π}{6}$个单位
	C．	向右平移$\frac{π}{3}$个单位		D．	向左平移$\frac{π}{3}$个单位

2．已知复数z=$\frac{1-2i}{3+4i}$（i是虚数单位），则z的共轭复数的虚部是（　　）

试题分类