题目内容
15.等腰△ABC中,AB=AC,D为AC中点,BD=1,则△ABC面积的最大值为$\frac{2}{3}$.分析 先在△ABD中利用余弦定理表示出cosA,进而求得sinA的表达式,进而代入三角形面积公式利用转化为二次函数来解决.
解答 解:cosA=$\frac{{b}^{2}+\frac{{b}^{2}}{4}-1}{2•b•\frac{1}{2}b}$=$\frac{5}{4}$-$\frac{1}{{b}^{2}}$,
△ABC面积S=$\frac{1}{2}$b2•$\sqrt{1-(\frac{5}{4}-\frac{1}{{b}^{2}})^{2}}$=$\frac{1}{8}$$\sqrt{-9({b}^{2}-\frac{20}{9})^{2}+\frac{256}{9}}$≤$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题主要考查了余弦定理和正弦定理的运用.解题过程中充分利用好等腰三角形这个条件,把表达式的未知量减到最少.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
3.定义在区间(a,a+2)上的奇函数y=f(x),当0<x<a+2时,f(x)=-($\frac{1}{2}$)x+$\frac{1}{2}$,则y的取值范围是(-$\frac{1}{2}$,0).
10.四面体ABCD的四个顶点均在半径为2的球面上,若AB、AC、AD两两垂直,$\overrightarrow{BA}•\overrightarrow{BC}$=2,则该四面体体积的最大值为( )
| A. | $\frac{7\sqrt{2}}{6}$ | B. | $\frac{7}{3}$ | C. | 2$\sqrt{2}$ | D. | 7$\sqrt{2}$ |
 如图所示,几何体ABCDE中,△ABC为正三角形,CD⊥面ABC,BE∥CD,BC=CD=2BE.
如图所示,几何体ABCDE中,△ABC为正三角形,CD⊥面ABC,BE∥CD,BC=CD=2BE.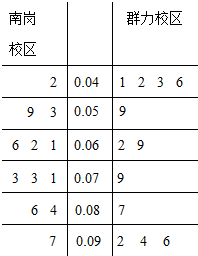 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )