题目内容
8.设a=log3π,b=log2$\sqrt{3}$,c=log3$\sqrt{2}$,则a、b、c的大小关系是( )| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | b>a>c |
分析 利用指数函数与对数函数的单调性即可得出.
解答 解:∵b=log2$\sqrt{3}$=$\frac{1}{2}lo{g}_{2}^{3}$,c=log3$\sqrt{2}$=$\frac{1}{2}lo{g}_{3}^{2}$,$lo{g}_{2}^{3}•lo{g}_{3}^{2}$=1,∴$2>lo{g}_{2}^{3}>lo{g}_{3}^{2}>0$,
∴c<b<1.
又a=log3π>1,
∴a>b>c.
故选:A.
点评 本题考查对数函数的单调性,属于基础题.

练习册系列答案
相关题目
16.非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则( )
| A. | $\overrightarrow{a}$与$\overrightarrow{b}$方向相同 | B. | $\overrightarrow{a}$与$\overrightarrow{b}$方向相反 | C. | $\overrightarrow{a}$与$\overrightarrow{b}$垂直 | D. | 以上都不对 |
3.定义在区间(a,a+2)上的奇函数y=f(x),当0<x<a+2时,f(x)=-($\frac{1}{2}$)x+$\frac{1}{2}$,则y的取值范围是(-$\frac{1}{2}$,0).
17.过椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的右焦点F作两条相互垂直的直线分别交椭圆于A,B,C,D四点,则$\frac{1}{|AB|}+\frac{1}{|CD|}$的值为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | 1 | D. | $\frac{7}{12}$ |
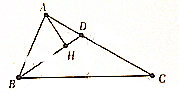 如图,在△ABC中,AC=12,∠ABC=2∠C.
如图,在△ABC中,AC=12,∠ABC=2∠C.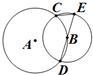 如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径.已知CE=1,DE=4,则圆A的半径为4.
如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径.已知CE=1,DE=4,则圆A的半径为4.