题目内容
14.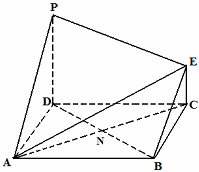 如图,已知几何体的底面ABCD 为正方形,AC∩BD=N,PD⊥平面ABCD,
如图,已知几何体的底面ABCD 为正方形,AC∩BD=N,PD⊥平面ABCD,PD=AD=2EC,EC∥PD.
(Ⅰ)求异面直线BD与AE所成角:
(Ⅱ)求证:BE∥平面PAD;
(Ⅲ)判断平面PAD与平面PAE是否垂直?若垂直,请加以证明;若不垂直,请说明理由.
分析 (Ⅰ)先证明出EC⊥平面ABCD,进而根据线面垂直的判定定理证明出BD⊥平面AEC,进而推断出BD⊥AE,可知直线所成的角为90°.
(Ⅱ)先利用面面平行的判定定理证明出平面BCE∥平面PAD,进而证明出线面平行.
(Ⅲ)先假设垂直,作PA中点F,连结DF,证明出DF⊥PA和DF⊥PE,利用线面垂直的判定定理证明出CD⊥平面PAD和DF⊥平面PDCE,确定∠PDF的值.
解答 解:(Ⅰ)PD⊥平面ABCD,EC∥PD,
∴EC⊥平面ABCD,
又BD?平面ABCD,
∴EC⊥BD,
∵底面ABCD为正方形,AC∩BD=N,
∴AC⊥BD,
又∵AC∩EC=C,AC,EC?平面AEC,
∴BD⊥平面AEC,
∴BD⊥AE,
∴异面直线BD与AE所成角的为90°.
(Ⅱ)∵底面ABCD为正方形,
∴BC∥AD,
∵BC?平面PAD,AD?平面PAD,
∴BC∥平面PAD,
∵EC∥PD,EC?平面PAD,PD?平面PAD,
∴EC∥平面PAD,
∵EC∩BC=C,EC?平面BCE,BC?平面BCE,∴
∴平面BCE∥平面PAD,
∵BE?平面BCE,
∴BE∥平面PAD.
(Ⅲ) 假设平面PAD与平面PAE垂直,作PA中点F,连结DF,
∵PD⊥平面ABCD,AD CD?平面ABCD,
∴PD⊥CD,PD⊥AD,
∵PD=AD,F是PA的中点,
∴DF⊥PA,
∴∠PDF=45°,
∵平面PAD⊥平面PAE,平面PAD∩平面PAE=PA,DF?平面PAD,
∴DF⊥平面PAE,
∴DF⊥PE,
∵PD⊥CD,且正方形ABCD中,AD⊥CD,PD∩AD=D,
∴CD⊥平面PAD.
又DF?平面PAD,
∴DF⊥CD,
∵PD=2EC,EC∥PD,
∴PE与CD相交,
∴DF⊥平面PDCE,
∴DF⊥PD,
这与∠PDF=45°矛盾,
∴假设不成立即平面PAD与平面PAE不垂直.
点评 本题主要考查了线面平行和线面垂直的判定定理的运用.考查了学生推理能力和空间思维能力.

| A. | -i | B. | -1 | C. | i | D. | 1 |
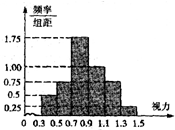 某班50名学生的高校招生体检表中的视力情况进行统计,其结果的频率分布直方图如图所示.若A高校某专业对视力的要求在1.1以上,则该班学生中能报A高校该专业的人数为( )
某班50名学生的高校招生体检表中的视力情况进行统计,其结果的频率分布直方图如图所示.若A高校某专业对视力的要求在1.1以上,则该班学生中能报A高校该专业的人数为( )| A. | 10 | B. | 20 | C. | 8 | D. | 16 |