题目内容
（13分）
在直角坐标系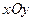
中，点M到点
的距离之和是4，点M的轨迹是C，直线
与轨迹C交于不同的两点P和Q.
（I）求轨迹C的方程；
（II）是否存在常数
？若存在，求出k的值；若不存在，请说明理由.
在直角坐标系
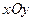中，点M到点的距离之和是4，点M的轨迹是C，直线与轨迹C交于不同的两点P和Q.（I）求轨迹C的方程；
（II）是否存在常数
？若存在，求出k的值；若不存在，请说明理由.（1）
的距离之和是4，
的轨迹C是长轴为4，焦点在x轴上焦距为
的椭圆，
其方程为
…………4分 （2）将
，代入曲线C的方程，
整理得
①
…………6分
设
由方程①，得
② …………8分
又
③
若
得
…………10分
将②、③代入上式，
解得
…………12分
又因k的取值应满足
即
（*），
将
代入（*）式知符合题意 …………13分
的距离之和是4，的轨迹C是长轴为4，焦点在x轴上焦距为的椭圆，
|
…………4分 （2）将，代入曲线C的方程，整理得
①…………6分
设
由方程①，得 ② …………8分又
③若
得
…………10分将②、③代入上式，
解得
…………12分又因k的取值应满足
即
（*），将
代入（*）式知符合题意 …………13分略
练习册系列答案
阅读快车系列答案
相关题目
，动点
满足
，
时，求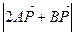
的最大值和最小值。
，
，
（
），
，O为坐标原点，若实数
使向量
，
和
满足：
，设点P的轨迹为
．
时，过点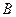
，能否在直线
上找到一点
，恰使
为正三角形？请说明理由．
上移动，等腰△OPA的顶角∠OPA为120°（O，P，A按顺时针方向排列），求点P的轨迹方程
，若点P满足
。
与点P的轨迹交于A、B两点，若
，且曲线E上存在点C，使
，求实数
，试在此区间内确定t的值，使图中的阴影部分面积s1与s2之和最小.
有公共点，则b的取值范围是
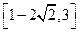
自由下落时，进入槽口
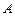处的概率为 
